Network flows: Ford-Fulkerson and Edmonds-Karp algorithms; max flow–min cut

Given some directed, weighted graph representing a network, where weights represent some capacity (e.g., vehicles per hour, liters of water per hour, etc.) it’s natural to ask “How much stuff(whatever that stuff is) can flow through the network between two nodes, the source (s) and the sink (t)?”

Given any graph, a “cut” is the removal of some subset of edges that disconnects two nodes in the network. In any given graph there may be many such cuts. Given some directed, weighted graph, and selecting two nodes, s and t, in this graph, we might ask “What is the minimum weight cut that disconnects s from t?”

It turns out that these two questions are related. In fact, they amount to the same thing. Given some directed, weighted graph and two nodes, s and t, the maximum flow between s and t supported by the network is exactly equal to the minimum weight of a cut that disconnects s and t. Why is this? Consider some cut which disconnects s and t. Flow from s to t must pass through at least some of these edges. If we can find a minimum weight cut disconnecting s and t, we can’t have flow greater than the weight of the cut. Hence, maximum flow is less than or equal to the weight of this cut. By the same token, if we consider the maximum flow through a network between s and t, then there cannot be any cut disconnecting s and t with greater weight. Therefore, the minimum weight cut is less than or equal to the maximum flow. If two things are both less than or equal to the other, then they must be equal! Hence, max flow equals min cut.

Network Flows, Part One: Max Flow-Min Cut; Ford-Fulkerson

Network Flows, Part Two: Ford-Fulkerson, continued

Resources and supplemental materials

• Max flow / min cut Theorem
• Network flows (Princeton University; also includes how we can use network flows to solve bipartite matchings)
• Ford-Fulkerson algorithm
• Edmonds-Karp algorithm
• Augmenting path
• NetworkFlows1.pdf
• NetworkFlows2.pdf

Comprehension check

1. True or false? An augmenting path is a path in a directed graph between two nodes that carries some flow between these two nodes.
2. True or false? Ford-Fulkerson is a greedy algorithm.
3. True or false? Every network will have at least one blocking flow.
4. True or false? The flow through an edge may temporarily exceed the capacity of the edge when flow into the starting node is sufficient.
5. True or false? The flow out of the source, must equal the flow into the sink.
6. True or false? Nodes in a network may store flow as in a buffer when in flow exceeds capacity for outflow.
7. True or false? Constructing the correct residual network is an essential step in solving for maximum flow.
8. True or false? If we don’t include “backward” edges in our residual network, it is possible for the Ford-Fulkerson algorithm to arrive at a solution that is less than the actual maximum flow for a network.
9. Given some network of directed edges, with the number of edges given by |E|, the correct residual graph will have ________________ edges.
10. True or false? The Ford-Fulkerson algorithm precisely determines the sequence in which augmenting paths will be discovered.

Answers: ǝslɐɟ[ / ]|Ǝ|ᄅ / ǝnɹʇ / ǝnɹʇ / ǝslɐɟ / ǝnɹʇ / ǝslɐɟ / ǝslɐɟ / ǝnɹʇ / ǝnɹʇ

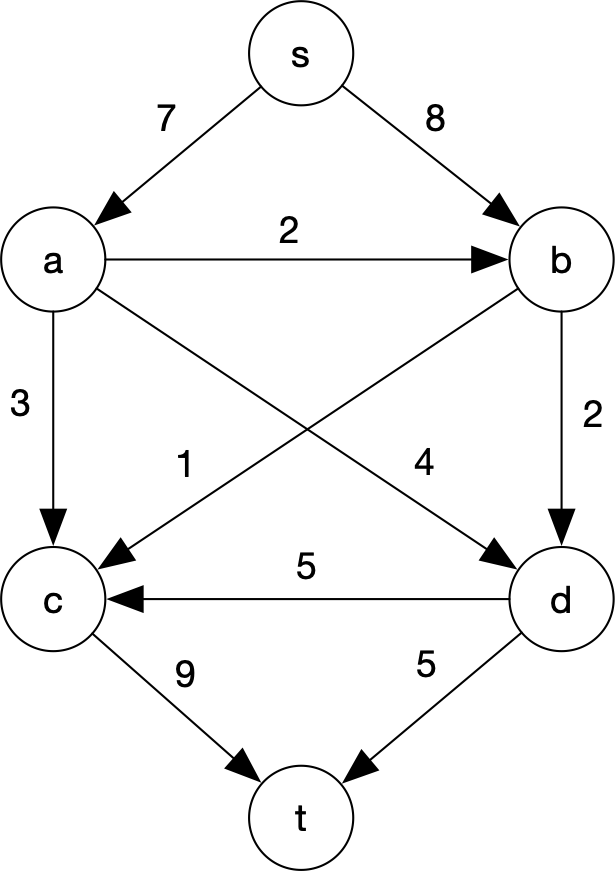
Practice: Make sure you can solve for maximum flow in a simple network using Ford-Fulkerson. Make up your own examples and solve them. Make sure you construct the correct residual network first. Here’s one problem instance to get you started.

Practice problem instance for Ford-Fulkerson

Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >

No generative AI was used in producing this material. This was written the old-fashioned way.

All materials copyright © 2020–2023, The University of Vermont. All rights reserved.