Shortest path: Dijkstra’s algorithm, Bellman-Ford algorithm

Published

2023-08-05

Dijkstra’s algorithm is one of the most famous—and useful—algorithms in all computer science. Given a weighted directed graph, G, and some starting node S, Dijkstra’s algorithm will find the shortest paths from S to all other nodes in the graph. One constraint on using Dijkstra’s algorithm is that all edge-weights must be non-negative.

Dijkstra’s algorithm

Dijkstra’s algorithm is great as long as we have no negative weight edges in our graph. But there are many problems for which it is natural to represent weights with positive and negative values—gains and losses, costs and profits, exothermic and endothermic chemical reactions, and so on.

Bellman-Ford algorithm

So what do we do when we have negative weights? As long as there are no negative cycles in our weighted directed graph we can use the Bellman-Ford algorithm. Like Dijkstra’s algorithm, it takes a graph, G, and some starting node S, and returns the shortest paths to all other nodes in the graph.

Resources and supplemental materials

Comprehension check

  1. True or false? Dijkstra’s algorithm can be used to find the shortest path from one node to all other nodes in a connected, weighted, directed graph, as long as all edge weights are non-negative.
  2. True or false? The Bellman-Ford algorithm can be used to find the shortest path from one node to all other nodes in any connected, weighted, directed graph.
  3. True or false? Dijkstra’s algorithm assumes that adding an edge to a path can never decrease the weight of the path.
  4. True or false? If we have a negative weight cycle in a graph, we could reduce the weight of a path between two nodes by traveling along the cycle multiple times.

Answers: ǝnɹʇ / ǝnɹʇ / ǝslɐɟ / ǝnɹʇ

Practice

Make sure you can work through all the steps of Dijkstra’s algorithm and the Bellman-Ford algorithm on simple graphs. Make up your own simple problems and solve them. Here are two to get you started.

Practice problem for Dijkstra’s algorithm:

Practice Dikjstras

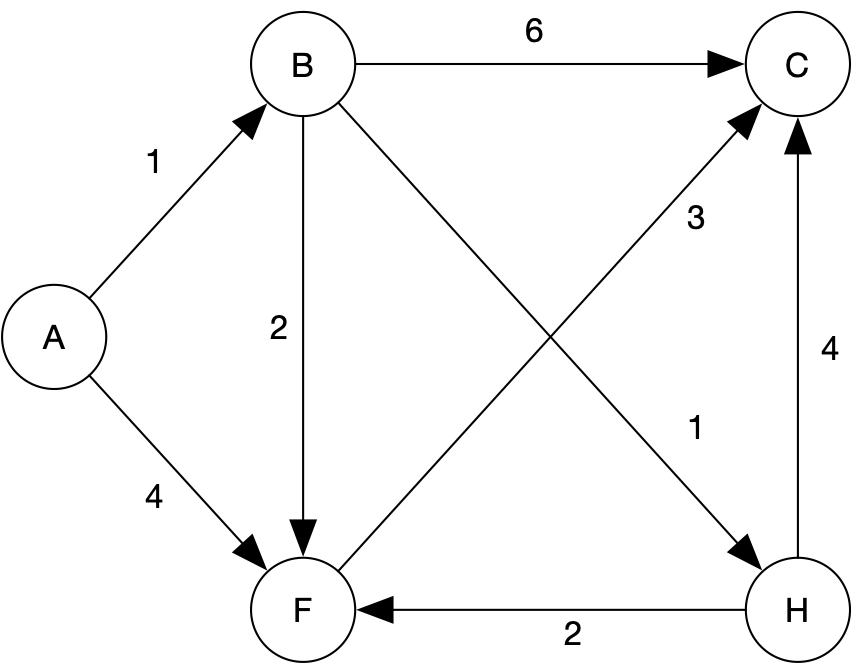
Practice problem for Bellman-Ford algorithm:

Practice problem instance for Bellman-Ford algorithm

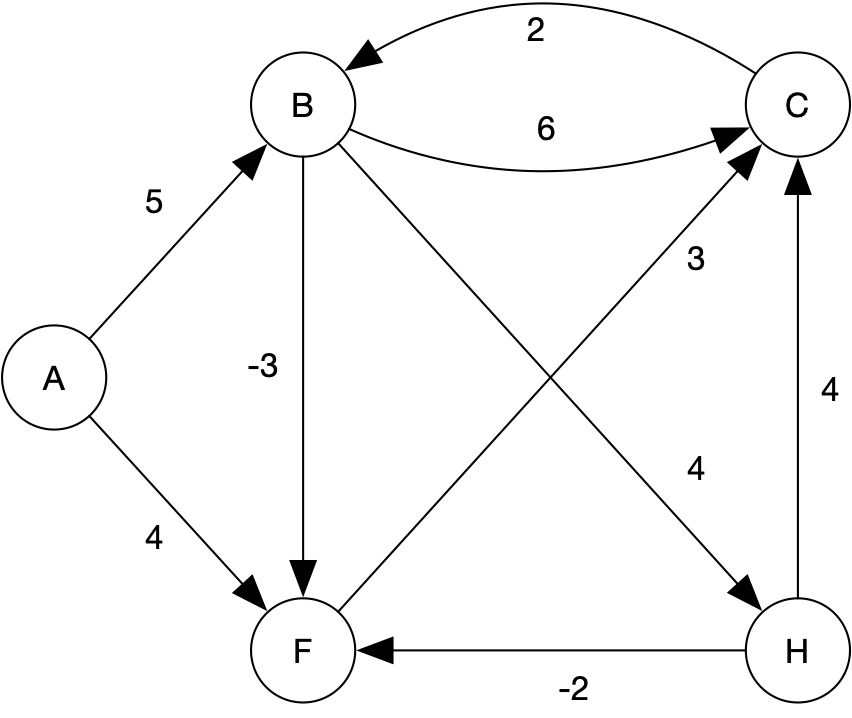
  • Could we use Bellman-Ford on the first problem above? Yes.

  • Which algorithm would be faster on the first problem above? Dijkstra’s.

  • Can we use Dijkstra’s algorithm on the second problem above? No.  Why not? Because the second graph includes edges with negative weights.

  • Does the graph in the second problem include any negative weight cycles? No. It does not.

Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >

No generative AI was used in producing this material. This was written the old-fashioned way.

All materials copyright © 2020–2023, The University of Vermont. All rights reserved.