Minimum spanning tree: Prim’s algorithm, Kruskal’s algorithm
You are the benevolent ruler of The Republic of Graphistan, and you want to modernize the roads between cities—widening them, repaving them, turning them into superhighways. But it’s complicated. When you look at a map of Graphistan you see that every city in your country is connected to every other country by some road. The situation at the treasury is looking a bit sketchy, so you want to minimize the cost of your new superhighway system. Surely this is a costly project! You decide—in your great wisdom—that every city should be connected to the new highway system, but that the amount of paving should be minimized. You consult with your ministers and (thankfully) one of them has studied algorithms. “What we need to do,” says the minister “is find a minimum spanning tree among all the roads connecting all the cities of Graphistan.” You think this is a wonderful idea—all the cities will be connected with the minimum amount of paved superhighway. Brilliant!
What is a minimum spanning tree? Let’s back up a bit, and define a spanning tree first. Ah, well, let’s back up a bit further and define a subgraph.
Given some graph G = (V, E) where V is the node (or vertex) set and E is the edge set, we say that a subgraph G', is a graph whose node set V' is a subset of V, and whose edge set E' is a subset of E. Obviously there are some constraints on this, for example, for every edge (u, v) in E', the end points of the edge, u and v, must be included in the node set V'. You can’t have an edge without its endpoints! So that’s a subgraph.
Now, what is a spanning tree? Given some graph G = (V, E), a spanning tree is a subgraph of G, call it G' = (V, E'), where the node set is the same as that in G, and the edge set, E' is a subset of E, and where G' is a tree—that is, on |V| nodes it must have exactly |V| - 1 edges, and it must be connected. That’s a spanning tree.
Now, what is a minimum spanning tree? If G is a weighted graph, then a minimum spanning tree is a spanning tree in which the sum of the weights of the edges in E' is minimized. That is, the sum of the weights of the edges in E'
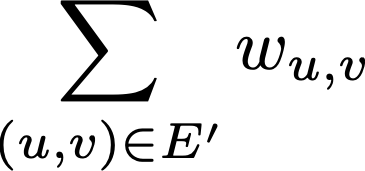
is minimized.
But how do you find such a minimum spanning tree? Prim and Kruskal to the rescue! These are two algorithms that solve the same problem, finding a minimum weight spanning tree in a connected graph. Either works, though they use different approaches.
Finding a minimum spanning tree using Prim’s algorithm (with some review regarding trees)
Resources and supplemental materials:
- MinimumSpanningTreePrim.pdf
- https://en.wikipedia.org/wiki/Minimum_spanning_tree
- https://en.wikipedia.org/wiki/Prim%27s_algorithm
Comprehension check:
- A tree is a connected, ________, undirected graph.
- Prim’s algorithm builds a vertex set and an edge set for the minimum spanning tree by iteratively finding the minimum weight edge with exactly one _______ in the vertex set constructed so far.
- True or false? Given some weighted, connected graph, G, Prim’s algorithm will find all minimum spanning trees of G.
- True or false? Given some weighted, connected graph G = (V, E), and a minimum spanning tree G' = (V, E'), if there is some edge (u, v) in E not in E', but of the same weight as some edge (w, y) in E' but not in E, we can always swap these edges to produce a new spanning tree of G.
- True or false? The edges of minimum spanning trees can have negative edge weights.
- True or false? Prim’s algorithm is a divide and conquer algorithm.
- True or false? Prim’s algorithm is a greedy algorithm.
- We can improve performance of Prim’s algorithm by using a/an __________ if the graph is sparse (that is, there is a low ratio of edges to nodes).
Answers: dɐǝɥ uᴉɯ / ǝnɹʇ / ǝslɐɟ / ǝnɹʇ / ǝslɐɟ / ǝslɐɟ / ʇuᴉodpuǝ / ɔᴉlɔʎɔɐ
Finding a minimum spanning tree using Kruskal’s algorithm
Supplemental materials:
- MinimumSpanningTreeKruskal.pdf
- https://en.wikipedia.org/wiki/Kruskal%27s_algorithm
Comprehension check:
- True or false? Given some weighted, connected graph, G, if there are multiple minimum spanning trees of G, Prim’s algorithm and Kruskal’s algorithm are guaranteed to find the same minimum spanning tree.
- True or false? Most of the work done in Kruskal’s algorithm is in updating the sum of weights when edges are added to the solution.
- Kruskal’s algorithm builds a solution by first sorting the edges (or adding them to a min heap) and then adding edges to E' unless they form a/an __________.
- True or false? Detecting a cycle in Kruskal’s algorithm can be done quickly and efficiently by using the disjoint sets find and union approach.
- Kruskal’s algorithm terminates when $|E’| = $ _____________.
- Given some weighted, connected graph G = (V, E), and an implementation of Kruskal’s algorithm using disjoint sets, and we are constructing a minimum weight spanning tree G' = (V, E'), then given some edge (u, v) in E not in E', if
find(u) == find(v)and we were to add (u, v) to E', then G' would contain a _________.
Answers: ǝlɔʎɔ / Ɩ - |Λ| / ǝnɹʇ / ǝlɔʎɔ / ǝslɐɟ / ǝslɐɟ
Copyright © 2023–2025 Clayton Cafiero
No generative AI was used in producing this material. This was written the old-fashioned way.