13 Data Simulation
Packages needed:
* tidyr
* rgdal
* ggplot2Welcome to Chapter 13! You’ve been analyzing the Tauntaun dataset throughout this primer, beginning with the two .csv files that were given to you way back in Chapter 5 (Projects). In previous chapters, we spent some time cleaning and merging the datasets, and then summarized the data and created a markdown annual report. We also analyzed the data using our sex-age-kill function and other basic statistical approaches. In this chapter, we’ll spill the beans and show you how two original csv datasets were created in R. The main purpose of this chapter is to show you how to simulate a dataset, and the key functions involved.
The first csv stores the Tauntaun harvest data, which we created by simulating Tauntaun population dynamics and harvest through time. This approach involves creating and working with arrays, using a few probability distributions for simulating data, and then using several of R’s data manipulation functions to create the final csv file. We’ve incorporated some typos along the way so that you could learn some functions that come in handy for proofing data. The second csv file stores hunter information, which if you remember, gave us practice merging two datasets.
WARNING: The “long chapter” warning is in full effect! This chapter introduces new material and makes extensive use of previous material as a review . . . make sure to give yourself time and take some breaks.
13.1 Population Model Overview
To create the Tauntaun harvest data, we need to simulate the Tauntaun population through time. We’ll set up a 10 year population simulation, where we will track the number of male and female Tauntauns separately in each time step (each year).
Tauntaun life history has been well studied by biologists on the icy planet of Hoth, and it’s reasonable to assume that life history characteristics are the same in Vermont. Individuals can begin breeding at the age of 1, and produce approximately 2 offspring per year. Individuals that are 0 years old are called “young” because they cannot breed. One-year-old breeders are called “recruits” because these individuals have been recruited into the breeding population. Older breeders (age 2+) are called “adults” because they are adult (experienced) breeders.
In a population model, nailing down the timing of events is absolutely critical. Here’s an overview of the Tauntaun timing of events . . .
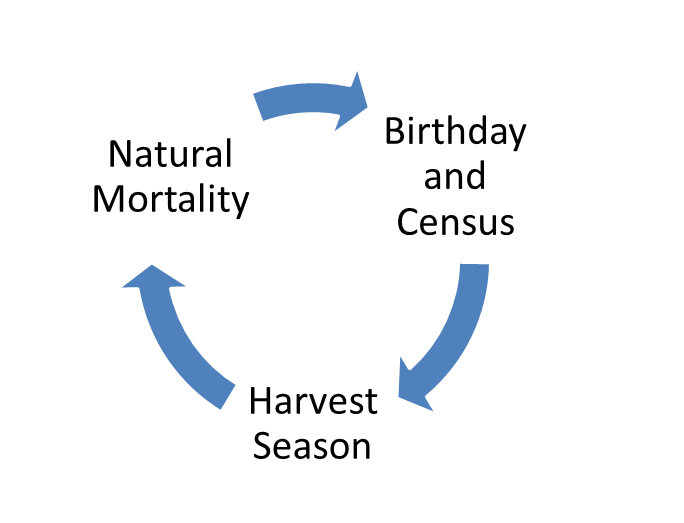
Figure 13.1: Tauntaun life cycle.
- The census (top) occurs on the birthday, which occurs before the harvest. All Tauntauns are born on the exact same day - August 1st. The census is a count of 0, 1, 2, 3, 4, 5 year males and females. Because the census includes 0-year-olds, this is referred to as a “post-breeding census”. All individuals counted at the census remain alive until the harvest.
- The harvest occurs in the fall, and the number of animals harvested depends on a harvest rate (harvest probability).
- After the harvest, there is a period of natural mortality. We’ll assume this natural mortality does not affect animals during the short harvest season.
- We’ve come full circle. Tauntauns that survive the harvest and the natural mortality period are able to give advance to the birthday again. On the birthday, the animals that were 0 years old are now 1, and they instantly give birth to ~ 2 offspring. The animals that were 1 years old are now 2, and they instantly give birth to ~2 offspring, etc. These “fresh” individuals are now counted for the year 2 census.
13.1.1 Simulation Inputs
We developed a Tauntaun population in a spreadsheet called SimHarvest_2020.xlsx. This file should be located in your simulations directory, and our goal now is to convert the spreadsheet model into an R script.
You may not remember this, but the main inputs to the model are given in two sections of the spreadsheet. In Chapter 5, you read in the Excel file and saved these inputs as a list. Then you saved the inputs as sim_inputs.Rdata. This should be located in your simulations directory. Let’s check that now, and read in the file with the load function:
## [1] TRUE# load in the file
load("simulations/sim_inputs.Rdata")
# check the structure of the object sim_inputs
str(sim_inputs)## List of 2
## $ pop.seed :'data.frame': 2 obs. of 7 variables:
## ..$ Sex: chr [1:2] "females" "males"
## ..$ 0 : num [1:2] 3000 1200
## ..$ 1 : num [1:2] 1500 900
## ..$ 2 : num [1:2] 500 300
## ..$ 3 : num [1:2] 300 180
## ..$ 4 : num [1:2] 100 60
## ..$ 5 : num [1:2] 50 30
## $ pop.params:'data.frame': 5 obs. of 7 variables:
## ..$ Rate: chr [1:5] "survival.f" "survival.m" "birth" "harvest.f" ...
## ..$ 0 : num [1:5] 0.400000000000000022204 0.400000000000000022204 0 0.000000000000000000001 0.000000000000000000001
## ..$ 1 : num [1:5] 0.7 0.7 2 0.2 0.3
## ..$ 2 : num [1:5] 0.8 0.8 2.5 0.2 0.3
## ..$ 3 : num [1:5] 0.9 0.9 2.5 0.2 0.3
## ..$ 4 : num [1:5] 0.9 0.9 2.5 0.2 0.3
## ..$ 5 : num [1:5] 0 0 2.5 0.2 0.3Does this ring a bell? We created sim_inputs.RData in Chapter 5, but you’re brain may be a bit cluttered right now! The inputs for our population model are stored in a list (sim_inputs) consisting of 2 objects (pop.seed, pop.params, each of which is a data.frame. Remember, because the information is stored in a list, we need to first tell R what section of the list we are referring to with double brackets [[ ]], and from there you can work with the enclosed object.
With sim_inputs loaded into R’s memory, we can now translate the Tauntaun life history characteristics into a population model. We’ll be running a 10 year simulation that has a 1 year time step.
13.2 The “pop” Array
Our model will hold numbers of individuals, tracked for each age and sex, at different stages of the life cycle. We’ll start with the census, and work through the life cycle in chronological order.
Here are the stages we’ll be tracking:
- census - number of individuals at the time of the population census,
- harvest - the number of individuals harvested,
- escapees - the number of individuals that escaped the harvest,
- survivors - the number of individuals that survive the natural mortality period.
We’ll need to keep track of all of these individuals for each year, and by age and sex. The best way to store this information is in an object that is an array, which we introduced in Chapter 4. Arrays can be thought of as multi-dimension vectors. They hold a single data type (in our case, numbers). Arrays have rows, columns, and can have multiple pages of rows and columns, much like an Excel workbook. The trick is how to give instructions to “snake” through the rows, columns, and pages in the correct order.
You can create an array with the array function. Let’s use the args function to look at this function’s arguments.
## function (data = NA, dim = length(data), dimnames = NULL)
## NULLFrom the output, we see that the first value in the argument list is the data. We can start by entering NA’s in the array, which indicates Not Available, and then replace them as we build the model. The second argument is called dim, which is where you specify the dimensions of your array. The default is length(data), but this won’t work for us. How many dimensions do we need? We’re tracking 10 years, 6 ages (ages 0-6), 2 sexes (m for male, and f for female), and 4 stages in the life cycle (census, harvest, escapees, and survivors). Remember that the order of the dimensions is critical for determining how the resulting array looks, as well as how you feed the array and extract from it. The order gives the direction in which to “snake” through the array to do calculations. So an array with dimensions as 10, 6, 2, 4 is organized differently than an array with dimensions 6, 2, 10, 4, even if they hold the same number of entries. Russell Crowe can help us remember that the first two numbers set the rows and columns of our array, but the last two entries show additional dimensions.
The last argument is called dimnames and it allows you to name each of the dimensions. We strongly encourage this practice. If you remember from Chapter 4, dimnames is stored as an attribute of the object, and the names are stored in a list. When creating an array, the order of the names needs to match the order of the dimensions perfectly. That is, the first name in the dimnames list indicates the row names, the second name in the dimnames list indicates the column names, and so on.
# create arrays for holding numbers
pop <- array(data = NA,
dim = c(10, 6, 2, 4),
dimnames = list(yr = 1:10,
age = 0:5,
sex = c('f','m'),
stage = c('census','harvest', 'escapees', 'survivors')))Now that we’ve created an array (an object called pop), let’s have a look at it.
## , , sex = f, stage = census
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, stage = census
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, stage = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, stage = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, stage = escapees
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, stage = escapees
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, stage = survivors
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, stage = survivors
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NAThat’s quite an array! We won’t need to look at the entire array in future steps, but it helps to see the whole thing when you first create one to verify that it has the dimensions you expect. Notice that there are a series of two-dimensional grids provided, with rows as years and columns as age. Each two dimensional grid is identified by both sex (“m” or “f”) and stage of the life cycle (“census”, “harvest”, “escapees”, “survivors”). Right now our array is filled with NA’s. We’ll have this filled in with real numbers in no time.
Instead of looking at the entire array, the str function can be used to see what this array is all about:
## logi [1:10, 1:6, 1:2, 1:4] NA NA NA NA NA NA ...
## - attr(*, "dimnames")=List of 4
## ..$ yr : chr [1:10] "1" "2" "3" "4" ...
## ..$ age : chr [1:6] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "f" "m"
## ..$ stage: chr [1:4] "census" "harvest" "escapees" "survivors"The first line of this output tells us what kind of data are in the array (num), and the section [1:10, 1:6, 1:2, 1:4] provides the dimensions. The next line of output, attr(*, “dimnames”)=List of 4 tells us that the names of each dimension are stored as an attribute for the object, pop. An object can have multiple attributes; the attribute called dimnames is a list that contains four objects (which are all character vectors). The four vectors within it are named yr, age, sex, and stage, and the $ that precedes the name suggests that these values are contained within the dimnames list. The output tells you the actual dimension names (such as “f” and “m”) are stored as a vector of characters (chr). You can add more attributes to the list if you want, as we did in Chapter 4.
If you want to extract specific attributes for the object, pop, use the attr function.
## $yr
## [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
##
## $age
## [1] "0" "1" "2" "3" "4" "5"
##
## $sex
## [1] "f" "m"
##
## $stage
## [1] "census" "harvest" "escapees" "survivors"If you’d like to see all of the attributes for the object, pop, use the attributes function. You’ll see that our array has another attribute called dim, which stores the array’s dimensions only.
## $dim
## [1] 10 6 2 4
##
## $dimnames
## $dimnames$yr
## [1] "1" "2" "3" "4" "5" "6" "7" "8" "9" "10"
##
## $dimnames$age
## [1] "0" "1" "2" "3" "4" "5"
##
## $dimnames$sex
## [1] "f" "m"
##
## $dimnames$stage
## [1] "census" "harvest" "escapees" "survivors"Hopefully it is sinking in that you must know how the array is arranged in order to work with it. We’ll leave our population array for now, and move onto the topic of rates. Then, we’ll use the rate data to help fill in our array called pop.
13.3 The “rates” Array
The Tauntaun population model requires that you specify vital rates, such as harvest rate, birth rate, and natural survival rate. We’ll track each of these rates by age, sex, and year, so we’ll need another array for holding these rates. One more vital rate is needed for our population model – the sex ratio of the offspring – but for this exercise they will be a constant 0.5 (50% of the offspring will be female, and 50% will be male), so we won’t need to add it to the array.
Let’s start by creating an object called rates with the array function. We’ll be tracking the three rates for each year, age and sex class. This time, our dimensions will be 10 years, 6 age classes, 2 sexes, and 3 rates, so we’ll set the dim argument to c(10, 6, 2, 3). The names of each dimension will be stored in a list, given in the exact same order as our dimensions: yr will run from 1:10, age will run between 0 and 5, sex will be “f” and “m”, and rate will be identified by “harvest”, “birth”, and “survival”. Remember, names in R are stored as characters, so ages will be stored as “0”, “1”, “2”, etc.
# create an object called rates that is an array
rates <- array(data = NA,
dim = c(10, 6, 2, 3),
dimnames = list(yr = 1:10,
age = 0:5,
sex = c('f','m'),
rate = c('harvest', 'birth','survival')))
# look at the structure of the object called rates
str(rates)## logi [1:10, 1:6, 1:2, 1:3] NA NA NA NA NA NA ...
## - attr(*, "dimnames")=List of 4
## ..$ yr : chr [1:10] "1" "2" "3" "4" ...
## ..$ age : chr [1:6] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "f" "m"
## ..$ rate: chr [1:3] "harvest" "birth" "survival"## , , sex = f, rate = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, rate = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, rate = birth
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, rate = birth
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, rate = survival
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = m, rate = survival
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NAAnother impressive array! Make sure to look at its length (360). We are going to fill in this array with numbers next. We’ll then use these rates to project the Tauntaun population through time.
13.3.1 Filling the Rates Array
The vital rates are currently stored in a dataframe called pop.params, which is part of the sim.inputs list. Let’s have a look.
## Rate 0 1 2 3 4 5
## 1 survival.f 0.400000000000000022204 0.7 0.8 0.9 0.9 0.0
## 2 survival.m 0.400000000000000022204 0.7 0.8 0.9 0.9 0.0
## 3 birth 0.000000000000000000000 2.0 2.5 2.5 2.5 2.5
## 4 harvest.f 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 5 harvest.m 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3This is a dataframe that stores vital rates by Tauntaun age class (0-5). The name of the rate is given in the first column. The first two rows give the natural survival rate of females and males, respectively, by age class. In row 3, the per capita birth rate is stored. This is the total number of offspring produced per female per year. Notice that Tauntauns >= 1 year old can breed. The final two rows give the harvest rate of females and males by age class.
Now it’s just a matter of moving these rates into their correct position in the rates array. Because the information above is stored as a dataframe, we’ll need to extract the row we need, and convert it to a matrix with the as.matrix function. Remember that an array (like a vector and matrix) can store a single datatype (mode or type) within it. Dataframes are lists, so they cannot be inserted into an array directly.
Let’s start with the female survival rates, which is stored in row 1 of our sim_inputs$pop.params object.
# extract the female survival rates by index
data <- as.matrix(sim_inputs$pop.params[1, 2:7])
# look at the data; it is a 1 row by 6 column matrix
data## 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0These are our age-specific female natural survival rates. If we assume that they are the same for all 10 years of the simulation, we can simply turn this into a 10 row by 6 column matrix.
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.4 0.7 0.8 0.9 0.9 0
## [2,] 0.4 0.7 0.8 0.9 0.9 0
## [3,] 0.4 0.7 0.8 0.9 0.9 0
## [4,] 0.4 0.7 0.8 0.9 0.9 0
## [5,] 0.4 0.7 0.8 0.9 0.9 0
## [6,] 0.4 0.7 0.8 0.9 0.9 0
## [7,] 0.4 0.7 0.8 0.9 0.9 0
## [8,] 0.4 0.7 0.8 0.9 0.9 0
## [9,] 0.4 0.7 0.8 0.9 0.9 0
## [10,] 0.4 0.7 0.8 0.9 0.9 0What happened here? We created a matrix with 10 rows and 6 columns, and passed into it our data matrix. This matrix consisted of only 6 values (the female survival rates by age), but R recycled these values by row.
This matrix can now be stuffed into its correct spot in our rates array. Let’s first remind ourselves of the structure of the rates array so that we know are indexing system:
## logi [1:10, 1:6, 1:2, 1:3] NA NA NA NA NA NA ...
## - attr(*, "dimnames")=List of 4
## ..$ yr : chr [1:10] "1" "2" "3" "4" ...
## ..$ age : chr [1:6] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "f" "m"
## ..$ rate: chr [1:3] "harvest" "birth" "survival"Oh, yeah, right - the ordering is yr, age, sex, rate. Our matrix already contains all years and ages in the correct order, so we only need to specify the sex (“f”) and rate (“survival”) to correctly fill in the data:
# insert the female harvest rate into the rates array.
rates[yr = , age = , sex = "f", rate = "survival"] <- data
# look at the female survival rate portion of the rates array
rates[yr = , age = , sex = "f", rate = "survival"]## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0We take the code rates[yr = , age = , sex = “f”, rate = “survival”] to read “dip into the rates array, all years, all ages to extract the survival rate of females”. Note that our code above including the names of each section of the array:
You don’t need to add the section name, however. As with functions, as long as you know the order of the array, you can extract what is needed without section names, like this:
## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0We’ll keep the names as it produces more readable code, but we mention this because many examples in the R helpfiles do not include names.
Try typing rates[ in your console or script, and then press the tab key. You should see some helpers appear that allow you to select a particular element in the array by name, such as “f” or “survival”. These are not the named sections of the array, such as yr, age, sex, or stage; rather they are actually the dimnames (names of the dimensions in the array itself). The tab may come in handy because it reminds you of the structure of the array object.
As an aside, it appears that R won’t throw an error if you use incorrect section names. For example, this code works:
# the rates array with incorrect use of section names
rates[mo = , shemp = , curly = "m", larry = "survival"] <- data
# look at the rates array with bad names
rates[larry = , mo = , curly = "m", shemp = "survival"]## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0However, for any extraction, you must specify the named elements (dimnames) correctly. For example, this code throws an error because there is no array element called “female”.
Error in rates[, , "female", "survival"] : subscript out of boundsYou can also extract by position index. For example, these two lines of code return the same result.
# extract female survival rates for all years, age class "0"
rates[yr = , age = "0", sex = "f", rate = "survival"]## 1 2 3 4 5 6 7 8 9 10
## 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4## 1 2 3 4 5 6 7 8 9 10
## 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4 0.4If you do extract by index, keep the str function close at hand so you know how the different elements are indexed. Note here that age “0” is the first element of the ages (0:5). This can be confusing!
OK, let’s continue filling the rates array. Let’s follow suit to add in the male natural survival rates, which as stored in row 2 of the sim_inputs$pop.params object.
# extract the male survival rates
data <- as.matrix(sim_inputs$pop.params[2, 2:7])
# expand the data to a 10 row by 6 column matrix
data <- matrix(data = data, nrow = 10, ncol = 6, byrow = TRUE)
# fill in the correct portion of the array
rates[yr = , age = , sex = "m", rate = "survival"] <- data
# look at the male survival rate portion of the rates array
rates[yr = , age = , sex = "m", rate = "survival"]## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0## 0 1 2 3 4 5
## 2 0.4 0.7 0.8 0.9 0.9 0You may be wondering what the number 2 is doing to the left of this output. When we subset the pop.params dataframe with sim_inputs$pop.params[2, 2:7], we specificially asked for row 2, columns 2:7 to be returned. The #2 is the remnant row name from this extraction.
Next, let’s fill in the female birth rates. Recall that these rates provide the number of offspring produced per female Tauntaun by age. The rates are currently stored in row 3 of the sim_inputs$pop.params object.
# extract the female birth rates
data <- as.matrix(sim_inputs$pop.params[3, 2:7])
# expand the data to a 10 row by 6 column matrix
data <- matrix(data = data, nrow = 10, ncol = 6, byrow = T)
# fill in the correct portion of the array
rates[yr = , age = , sex = "f", rate = "birth"] <- data
# look at the female birth rate portion of the rates array
rates[yr = , age = , sex = "f", rate = "birth"]## age
## yr 0 1 2 3 4 5
## 1 0 2 2.5 2.5 2.5 2.5
## 2 0 2 2.5 2.5 2.5 2.5
## 3 0 2 2.5 2.5 2.5 2.5
## 4 0 2 2.5 2.5 2.5 2.5
## 5 0 2 2.5 2.5 2.5 2.5
## 6 0 2 2.5 2.5 2.5 2.5
## 7 0 2 2.5 2.5 2.5 2.5
## 8 0 2 2.5 2.5 2.5 2.5
## 9 0 2 2.5 2.5 2.5 2.5
## 10 0 2 2.5 2.5 2.5 2.5## 0 1 2 3 4 5
## 3 0 2 2.5 2.5 2.5 2.5Finally, let’s fill in the harvest rates. Recall that these rates provide the probability that a Tauntaun will be harvested by age class. The rates are currently stored in rows 4 and 5 of the sim_inputs$pop.params object. let’s remind ourselves what this looks like:
## Rate 0 1 2 3 4 5
## 1 survival.f 0.400000000000000022204 0.7 0.8 0.9 0.9 0.0
## 2 survival.m 0.400000000000000022204 0.7 0.8 0.9 0.9 0.0
## 3 birth 0.000000000000000000000 2.0 2.5 2.5 2.5 2.5
## 4 harvest.f 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 5 harvest.m 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3Next, let’s fill in the female harvest rates. The rates are currently stored in row 4 of the sim_inputs$pop.params object.
# extract the female harvest rates
data <- as.matrix(sim_inputs$pop.params[4, 2:7])
# expand the data to a 10 row by 6 column matrix
data <- matrix(data = data, nrow = 10, ncol = 6, byrow = TRUE)
# fill in the correct portion of the array
rates[yr = , age = , sex = "f", rate = "harvest"] <- data
# look at the male survival rate portion of the rates array
rates[yr = , age = , sex = "f", rate = "harvest"]## age
## yr 0 1 2 3 4 5
## 1 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 2 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 3 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 4 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 5 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 6 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 7 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 8 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 9 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 10 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2## 0 1 2 3 4 5
## 4 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2Finally, let’s fill in the male harvest rates. The rates are currently stored in row 5 of the sim_inputs$pop.params object.
Try this on your own! The main section to fill is rates[yr = , age = , sex = “m”, rate = “harvest”], and we are referencing row 5, columns 2:7 for the data. Your results should look like this:
## age
## yr 0 1 2 3 4 5
## 1 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 2 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 3 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 4 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 5 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 6 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 7 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 8 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 9 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 10 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3## 0 1 2 3 4 5
## 5 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3How did you do? Let’s have a look at our rates array once more in full.
## , , sex = f, rate = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 2 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 3 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 4 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 5 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 6 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 7 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 8 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 9 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
## 10 0.000000000000000000001 0.2 0.2 0.2 0.2 0.2
##
## , , sex = m, rate = harvest
##
## age
## yr 0 1 2 3 4 5
## 1 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 2 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 3 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 4 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 5 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 6 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 7 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 8 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 9 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
## 10 0.000000000000000000001 0.3 0.3 0.3 0.3 0.3
##
## , , sex = f, rate = birth
##
## age
## yr 0 1 2 3 4 5
## 1 0 2 2.5 2.5 2.5 2.5
## 2 0 2 2.5 2.5 2.5 2.5
## 3 0 2 2.5 2.5 2.5 2.5
## 4 0 2 2.5 2.5 2.5 2.5
## 5 0 2 2.5 2.5 2.5 2.5
## 6 0 2 2.5 2.5 2.5 2.5
## 7 0 2 2.5 2.5 2.5 2.5
## 8 0 2 2.5 2.5 2.5 2.5
## 9 0 2 2.5 2.5 2.5 2.5
## 10 0 2 2.5 2.5 2.5 2.5
##
## , , sex = m, rate = birth
##
## age
## yr 0 1 2 3 4 5
## 1 NA NA NA NA NA NA
## 2 NA NA NA NA NA NA
## 3 NA NA NA NA NA NA
## 4 NA NA NA NA NA NA
## 5 NA NA NA NA NA NA
## 6 NA NA NA NA NA NA
## 7 NA NA NA NA NA NA
## 8 NA NA NA NA NA NA
## 9 NA NA NA NA NA NA
## 10 NA NA NA NA NA NA
##
## , , sex = f, rate = survival
##
## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0
##
## , , sex = m, rate = survival
##
## age
## yr 0 1 2 3 4 5
## 1 0.4 0.7 0.8 0.9 0.9 0
## 2 0.4 0.7 0.8 0.9 0.9 0
## 3 0.4 0.7 0.8 0.9 0.9 0
## 4 0.4 0.7 0.8 0.9 0.9 0
## 5 0.4 0.7 0.8 0.9 0.9 0
## 6 0.4 0.7 0.8 0.9 0.9 0
## 7 0.4 0.7 0.8 0.9 0.9 0
## 8 0.4 0.7 0.8 0.9 0.9 0
## 9 0.4 0.7 0.8 0.9 0.9 0
## 10 0.4 0.7 0.8 0.9 0.9 0Don’t worry about the male birth rate section containing NA – male Tauntauns don’t give birth. We’ll be using this array for our Tauntaun population simulation soon. But first, let’s have a quick break:
Figure 13.2: Time for a break.
13.4 Stepping through the Life Cycle
Now that all of our rates are calculated, we’re ready to use them to project the population size through time, filling in our pop array. Let’s remind ourselves of the timing of events in the Tauntaun life cycle.

Figure 13.3: Tauntaun life cycle.
Don’t forget the life cycle is an annual cycle, but we must start somewhere. Our starting point will be called the “census”, which is when we count individuals in the population. This census will occur on the birth day, all Tauntauns are born on this day. So a 0 year old is a freshly born Tauntaun, a 1 year is a Tauntaun who is celebrating their first birthday, and so on. This structure is known as a post-breeding census because we count all individuals immediately after they are born. We assume that there are no deaths between the birthday and the harvest, which occurs in the fall. When a Tauntaun biologist analyzes the harvest data, which contains information about dead Tauntans, their analyses reveal something about the living Tauntaun population size immediately before the harvest began. After the harvest is a period of natural survival (one minus the natural survival rate is the natural mortality rate). Any Tauntauns that escape the harvest and escape natural mortality are able to reproduce on their birthdays, and we’ve come full cycle.
The model should be pretty straight forward, and has the following sequence:
- Census animals - this is the count of 0-5 year-old animals in each time step. We need to provide this number for the very first year, and thereafter the numbers are calculated.
- Harvest animals - we will harvest animals according to their harvest probability.
- Natural survival - after the harvest, animals will survive to breeding according to their natural survival rate.
- An we’re back to the birthday and census. Those females that survive the harvest and survive the natural mortality period then give birth. The number of offspring per breeding female is determined by the birth.rate. The numbers of 0-year-old males and 0-year-old females is established by the sex.ratio, which we will assume is 50-50. Immediately after the birthday, the population can be counted in year 2.
- Do you feel a loop coming on?
13.4.1 The Population Seed
The population model starts with what is called a “population seed”. This is the number of individuals at the start of our population model for all age and sex classes. You can’t create individuals out of thin air!
The population seed is stored in sim_inputs$pop.seed:
## Sex 0 1 2 3 4 5
## 1 females 3000 1500 500 300 100 50
## 2 males 1200 900 300 180 60 30This is another dataframe, with the starting female population size by ageclass stored in row 1, and the starting male population size stored in row 2. We’ll need to extract this content and add it to the pop array. Before we do that, it is useful to remind ourselves what this array is all about, and how it is structured:
## logi [1:10, 1:6, 1:2, 1:4] NA NA NA NA NA NA ...
## - attr(*, "dimnames")=List of 4
## ..$ yr : chr [1:10] "1" "2" "3" "4" ...
## ..$ age : chr [1:6] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "f" "m"
## ..$ stage: chr [1:4] "census" "harvest" "escapees" "survivors"OK, knowing the structure, let’s now add in the population seed:
# fill in the female population seed
female.seed <- as.matrix(sim_inputs$pop.seed[1, 2:7])
pop[yr = 1, age = , sex = "f", stage = "census"] <- female.seed
# fill in the male population seed
male.seed <- as.matrix(sim_inputs$pop.seed[2, 2:7])
pop[yr = 1, age = , sex = "m", stage = "census"] <- male.seed
# have a look
pop[yr = 1, age = , sex = , stage = "census"]## sex
## age f m
## 0 3000 1200
## 1 1500 900
## 2 500 300
## 3 300 180
## 4 100 60
## 5 50 30With our population seeded, we are now ready to begin. From here on out, all of our Tauntaun numbers through time will be calculated.
Before we actually write our simulation loop code, it will be useful to have an understanding of how the Tauntaun numbers will be calculated for each stage in one life cycle iteration. We’ll track the females only in the rest of this section so that you see the 1st year of the life cycle in its entirety. After that, we’ll start from the beginning and code the entire Tauntaun simulation as a loop.
13.4.2 The Harvest Season
To begin, to calculate the number of female Tauntauns harvested in year 1, we can multiply the census number of individuals of a specific age and sex class by their respective harvest probabilities. This is easy to accomplish….you just need to use the correct indexing for both the pop array and the rates array.
# look at the female seed population in year 1:
# these represent the females that can potentially be harvested;
pop[yr = 1, age = , sex = "f", stage = "census"] ## 0 1 2 3 4 5
## 3000 1500 500 300 100 50## 0 1 2 3 4 5
## 0.000000000000000000001 0.200000000000000011102 0.200000000000000011102 0.200000000000000011102 0.200000000000000011102 0.200000000000000011102Next, we’ll perform element-by-element multiplication to get the number of harvested animals. We’ll round these values to 0 with the round function (rounding to 0 digits, the default). This is done only so that we don’t harvest a fraction of an individual.
# fill in the year 1 female harvest
pop[yr = 1, age = , sex = "f", rate = "harvest"] <-
round(pop[yr = 1, age = , sex = "f", stage = "census"] *
rates[yr = 1, age = , sex = "f", rate = "harvest"])
# look at the number of harvested females
pop[yr = 1, age = , sex = "f", rate = "harvest"] ## 0 1 2 3 4 5
## 0 300 100 60 20 10You should be able to verify that the number harvested is the number of individuals times their harvest rate for each class.
However, our model will include stochasticity - that is, we would like to introduce elements of randomness to our model. We do so here not because we really want a stochastic Tauntaun population model (we really don’t need this complexity), but because it provides us an opportunity to show you, the reader, how to use if-else coding structures, describe random number seeds, and introduce some basic probability functions in R.
13.4.2.1 The Binomial Distribution
Instead of simply multiplying the census by the harvest rate (with accompanying rounding) to compute our harvested individuals, we will instead make use of the the binomial distribution. Let’s quickly introduce the binomial distribution now. Of course, our first stop will be the distribution’s help page:
Scan the helpfile, and you should see that there are 4 functions related to the binomial distribution: dbinom, pbinom, qbinom and rbinom. We will use two of these in our Tauntaun simulation (qbinom and rbinom).
In a nutshell, the shape of a binomial distribution is controlled by two parameters: the probability of success and the number of trials. For example, if we set the probability of success to 0.5 (and take this to mean the probability of harvest) and the number of trials to 10 (and take this to mean 10 Tauntauns), the binomial distribution looks like this:
plot(x = 0:10,
y = dbinom(0:10, 10, prob = 0.5, log = F),
main = "Binomial Distribution: n = 10, p = 0.5",
xlab = "Harvested Tauntauns out of 10 Total",
ylab = "Probability", col = "Red",
type = "h")
This is a binomial distribution for p (the probability of success, which R calls “prob”) = 0.5 and n (the number of trials is 10, which R calls “size”). On the x-axis, we have the number of harvested Tauntauns, and the y-axis is probability. From this graph, we can see that the probability of harvesting, say, 4 Tauntans out of 10, given a harvest rate of 0.5 is 0.205. If we were to sample from this distribution, can you see that it would be less likely to harvest, say, 0 or 10 Tauntauns (which are near the tails of the distribution) than to harvest 5 Tauntauns (which is towards the middle of the distribution)? The most likely number of harvested animals is 0.5 * 10, which is 5 Tauntauns. You can get the most likely value with the qbinom function, and setting the argument called p to 0.5 (in case you were wondering, this will return the middle of the cumulative binomial distribution):
## [1] 5Change the parameters of the binomial function, and you get a different binomial distribution. For example, here is a binomial distribution where p (the probability of success, which again we take to mean the probability of harvest) is 0.2:
plot(x = 0:10,
y = dbinom(0:10, size = 10, prob = 0.2, log = F),
main = "Binomial Distribution: n = 10, p = 0.2",
xlab = "Harvested Tauntauns out of 10 Total",
ylab = "Probability", col = "Red",
type = "h")
Here, with the probability of harvest set at 0.2, and 10 Tauntauns available to be harvested, it is much more likely that we will observe 0, 1, 2, 3, or 4 Tauntauns compared to 7, 8, 9, or 10 Tauntauns. Again, we can use the qbinom function to return the most likely value:
## [1] 2Suppose we would like to make the harvest stochastic. How exactly do you sample from this distribution? In Excel, you may have used the “BINOM.INV” function and set the argument named Alpha to a random number if you want a stochastic draw:
Figure 13.4: The BINOM.INV function in Excel.
In R, we use the rbinom function, where the letter r is a tip that we will be drawing random values from a distribution. Let’s look at this function’s arguments:
## function (n, size, prob)
## NULLHere, n is the number of samples to draw, and size and prob define which binomial distribution is of interest. Now, let’s draw 15 random values from a binomial distribution whose trials (size) = 10 and probability of success (prob) = 0.2.
## [1] 3 2 3 1 1 1 3 4 3 1 1 1 3 1 1Note that each result is an integer…you can’t get 1.5 harvested animals out of 10 trials.
13.4.2.2 Random Number Seeds
Let’s run the exact same code again two more times, and compare results:
## [1] 4 8 5 5 6 6 5 4 3 6 4 5 3 5 3## [1] 5 7 4 9 5 7 6 7 3 6 7 6 6 4 5What happened here? Well, when you ran rbinom with the exact same arguments, you very likely got two different results. That’s the heart of the function . . . it is a random draw. Most software programs, including R, have random number generators that aren’t truly random. Instead, they are called “pseudo random numbers”, which are random numbers that are obtained by using an algorithm (a set of rules). Check out this site for more background information, which has this to say:
A pseudorandom number generator (PRNG), also known as a deterministic random bit generator (DRBG), is an algorithm for generating a sequence of numbers that approximates the properties of random numbers. The sequence is not truly random in that it is completely determined by a relatively small set of initial values, called the PRNG’s state, which includes a truly random seed. Although sequences that are closer to truly random can be generated using hardware random number generators, pseudorandom numbers are important in practice for their speed in number generation and their reproducibility.
R has many functions that allow you to draw random values from a variety of probability distributions (the binomial distribution is just one of them). Because it’s nice to be able to reproduce your simulations exactly, R has a set.seed function. If you set the random number seed before you run the function, you should be able to get the exact same random sample. Take a look:
# now set the seed, choose any number, say 42
set.seed(42)
# and run it the first time
rbinom(n = 10, size = 10, prob = 0.5)## [1] 7 7 4 7 6 5 6 3 6 6# set the seed before you call the function
set.seed(42)
# run the code again
(samples <- rbinom(n = 10, size = 10, prob = 0.5))## [1] 7 7 4 7 6 5 6 3 6 6Same result! The bottom line is that if you need to recreate your simulation exactly, you must use the set.seed function.
Back to the female Tauntaun harvest. Earlier, we calculated our harvested population size by multiplying the year 1 female census by the year 1 female harvest rate:
# fill in the year 1 female harvest
pop[yr = 1, age = , sex = "f", rate = "harvest"] <-
round(pop[yr = 1, age = , sex = "f", stage = "census"] *
rates[yr = 1, age = , sex = "f", rate = "harvest"])
# look at the number of harvested females
pop[yr = 1, age = , sex = "f", rate = "harvest"] ## 0 1 2 3 4 5
## 0 300 100 60 20 10Now let’s use the binomial distribution functions instead. First, let’s create a new object called stoch.harvest. This object will have a logical datatype whose value will be TRUE if we wish the harvest to be stochastic and FALSE if not.
If stoch.harvest is FALSE, we will use qbinom to get the number of harvested females in year 1, like this:
qbinom(p = 0.5,
size = pop[yr = 1, age = , sex = "f", stage = "census"],
prob = rates[yr = 1,age = , sex = "f", rate = "harvest"])## 0 1 2 3 4 5
## 0 300 100 60 20 10Alternatively, if stoch.harvest is TRUE, we will use rbinom to get the number of harvested females in year 1. We only want 1 random draw for each age class. But we’ll take advantage of the fact that R can run rbinom in a vectorized manner if we feed it a vector of six 1’s (representing a single draw from each age class), a vector of trials (representing the number of females in each age class, stored in pop[1,,“f”,“census”]), and a vector of probabilities (representing the harvest probability for each age class, stored in rates[1,,“f”,“harvest”]):
# now use rbinom to make a single draw from a binomial distribution for each age class
rbinom(n = rep(1, times = 6),
size = pop[yr = 1, age = , sex = "f", stage = "census"],
prob = rates[yr = 1,age = , sex = "f", rate = "harvest"])## [1] 0 298 96 52 27 613.4.2.3 If-Else Coding
We’re at a point in our population model code where we need to implement the harvest, but we need to execute this in one of two ways, depending on whether the harvest is stochastic or not. We need an if-then function to help us through this. If you’ve used Excel, you’ve seen the IF function, which has three arguments:
Figure 13.5: The IF function in Excel.
In the first argument you enter a logical test (in our case, is stoch.harvest == TRUE). In the second argument, you enter what Excel should return if the logical test is true. In the third argument, you enter what Excel should return if the logical test is false.
R has a similar structure for if-then-else coding:
- Begin your code with the word if.
- Then enter your logical test within a set of parentheses.
- Then, tell R what to do if the logical test is true within a set of braces { }.
- Then enter the word else.
- Then tell R what to do in a second set of braces.
In words, it will look something like this:
if(stoch.harvest == TRUE) {
use rbinom() to generate the number harvested
}
else {
use qbinom() to generate the number harvested
}Let’s try it to get our total female harvest in year 1:
if (stoch.harvest == TRUE) {
pop[yr = 1, age = , sex = "f", stage = "harvest"] <- rbinom(n = rep(1, times = 6),
size = pop[yr = 1, age = , sex = "f", stage = "census"],
prob = rates[yr = 1,age = , sex = "f", rate = "harvest"])
} else
{
pop[yr = 1, age = , sex = "f", stage = "harvest"] <- qbinom(p = 0.5,
size = pop[yr = 1, age = , sex = "f", stage = "census"],
prob = rates[yr = 1,age = , sex = "f",rate = "harvest"])
} # end if
# look at the number harvested in year 1
pop[year = 1, age = , sex = "f", stage = "harvest"] ## 0 1 2 3 4 5
## 0 300 100 60 20 10Your numbers should match ours because stoch.harvest is currently set to FALSE. Notice that it is helpful to align your braces and add comments so that you can find sections within this code easily. Also note that RStudio allows you to “collapse” the code by pressing the little down-arrow to the right of the code line number. This collapses the IF function code so that you can hide portions of it if your code is getting too “thick”. Try it!
13.4.3 Computing Non-Harvested Totals
After the harvest is over, our surviving females should be counted. We’ve named these “escapees” and we’ll store them in the pop array under the “escapees” section.
## num [1:10, 1:6, 1:2, 1:4] 3000 NA NA NA NA NA NA NA NA NA ...
## - attr(*, "dimnames")=List of 4
## ..$ yr : chr [1:10] "1" "2" "3" "4" ...
## ..$ age : chr [1:6] "0" "1" "2" "3" ...
## ..$ sex : chr [1:2] "f" "m"
## ..$ stage: chr [1:4] "census" "harvest" "escapees" "survivors"We can calculate the number of escapees as the number in the census minus the number harvested.
# fill in the female escapees by subtraction
(pop[1,,"f","escapees"] <- pop[yr = 1, , "f", "census"] - pop[yr = 1, , "f", "harvest"])## 0 1 2 3 4 5
## 3000 1200 400 240 80 40These are the lucky female Tauntauns that escaped the harvest in year 1.
13.4.4 The Natural Survival Period
Now that the harvest is over, let’s continue to follow our “seed” population through the first time step of our model. The next phase deals with natural survival. If you recall, after the harvest is over, some Tauntauns will die of natural causes. As Hans Solo discovered, even Tauntauns can freeze to death! This portion of the model is not stochastic, and we could simply multiply the escapees times their natural survival rate to give us the number that survive this period. However, let’s put the qbinom function back to work:
pop[yr = 1, age = , sex = "f", stage = "survivors"] <- qbinom(p = 0.5,
size = pop[yr = 1, age = , sex = "f", stage = "escapees"],
prob = rates[yr = 1,age = , sex = "f",rate = "survival"])
# look at the number of survivors in year 1
pop[year = 1, age = , sex = "f", stage = "survivors"] ## 0 1 2 3 4 5
## 1200 840 320 216 72 0The 0 entry for 5 years olds is correct: Tauntauns cannot survive to their 6th birthday. However, all of the other age classes will advance 1 level on their birthday,
13.4.5 Birth Rates and Census
When individuals advance 1 age class on their birthday, the following birth rates will apply to females:
## 0 1 2 3 4 5
## 0.0 2.0 2.5 2.5 2.5 2.5These are the per capita birth rates for individuals that just had their birthday. A “fresh” 3-year-old female Tauntan will give birth to 2.5 offspring each year, on average.
However, we can’t simply do element by element multiplication here to get the total births produced by age class. Why not? Because we need to offset the population vector to advance individuals (i.e., get rid of the current 5 year olds), and we further need to lop off the 0-year old birth rate. Thus, to compute total births, we must consider these offsets. We can do so with the help of the head and tail functions, as shown below:
# get the first five entries from the pop array
breeders <- head(pop[year = 1, age = , sex = "f", stage = "survivors"], n = 5)
# get the last five entries from the rates array
birth.rates <- tail(rates[1, , "f", "birth"], n = 5)
# compute the total births by age class by vector multiplication
births <- round(breeders * birth.rates)These are the total births produced by each age class. If we assume a 50-50 sex ratio, we can use the qbinom to allocate these offspring by sex, as follows:
# compute the male offspring with the qbinom function
(male.offspring <- qbinom(p = 0.5, size = births, prob = 0.5))## 0 1 2 3 4
## 1200 1050 400 270 90# compute the female offspring as the total births minus male.offspring
(female.offspring <- births - male.offspring)## 0 1 2 3 4
## 1200 1050 400 270 90That brings us through an entire year for our seed cohort.
13.4.6 Year 2 Census
We’ve actually done the calculations for year 2 census . . . you just might not realize it yet. What would our population look like in year 2?
- Well, since the birthday is on the census, we can assume that all of the young produced by our population seed females would be counted as 0-year-olds in year 2.
- What about the number of 1-year-olds? The number of one year olds in year 2 would be the number of 0-year-olds in year 1 that escaped harvest and survived through the natural mortality period. These numbers are currently stored in ‘survivors’ portion of our pop array.
- What about the number of 2-year-olds? The number of 2-year-olds in year 2 depends on the number of 1-year-olds from the seed that escaped the harvest and survived to the year 2 census. These numbers are currently stored in ‘survivors’ portion of our pop array.
- Same goes for the 3 and 4-year-olds.
- The age 5 individuals are assumed to die and are not counted.
13.5 Looping in R
It would be very inefficient to enter calculations for year 2 because we’d have to enter them again for years 3, 4, . . . 10 of the simulation. What this needs is a loop . . . a coding structure that allows a certain set of instructions to be repeated over and over again until we tell it when to stop.
R offers a handful of loop options. If we wanted the loop to iterate until a certain criterion is met, we would use a while loop. However, in our population model, we know we want 10 years for a population simulation, so we can define exactly how many iterations we need the loop to pass through to populate the pop array. To do this, we use a for loop.
Let’s remind ourselves about R’s looping structure, and see a for loop in action.
## [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v" "w" "x" "y" "z"# allocate an empty vector that will store results of the loop
output <- vector(length = length(letters), mode = "character")
# loop through each element of numbers, and add the number 1 to it
for (i in 1:length(letters)) {
output[i] <- paste(letters[i], "_out")
}
# look at the object, numbers
output## [1] "a _out" "b _out" "c _out" "d _out" "e _out" "f _out" "g _out" "h _out" "i _out" "j _out" "k _out" "l _out" "m _out" "n _out" "o _out" "p _out"
## [17] "q _out" "r _out" "s _out" "t _out" "u _out" "v _out" "w _out" "x _out" "y _out" "z _out"The for loop has the following code structure:
- the word “for” starts the loop
- this is followed by a set of parentheses, inside of which there is an identifier that identifies which loop you are on. Here, we named our identifier i (for iteration). We could have named it something more descriptive if we wished. The code, i in 1:10, means we’ll let i take on the values 1 through 10. When the loop starts, a new variable called i will be created, and it will have a value of 1.
- this is followed by a set of braces { }, inside of which is code that specifies what to do. Here, we’ll take the vector, letters, and we’ll extract the ith element from it and paste "_out" to the end of it. For example, if we are on loop # 4 (i = 4), we’ll extract the fourth element from letters (d) and paste "_out" to it, creating the output “d_out” as the fourth element of the results vector.
In the next section, we’ll use a loop to create our final Tauntaun population model.
13.6 Final Tauntaun Population Model
Are you ready to add a loop and finalize our Tauntaun population model? We’ll run the entire code in one code “chunk” because R can’t break the loop (unless you are in a function and are using a debugger). We’ve been through each and every step of this model…the main difference is that we are going to put it all together in a loop.
At the beginning of our code, we set stoch.harvest to be TRUE or FALSE. We also reset our pop array, and select a random number seed so that we can reproduce our simulation completely.
The loop code starts with for (i in 1:10) {. This sets up a for loop for each year in our simulation. In the very first block of code, if(i == 1) evaluates to true, so the population seed for males and females will be entered into the pop array, and the else will be ignored. Then we move to step 2, which is the harvest. Here, we have an if code that carries out the harvest depending on whether the harvest is stochastic or not. Then we move to step 3, which simply counts the escapees. In step 4, we use the qbinom function to calculate the number of individuals who survive the natural mortality period. This ends our loop for i = 1, and i will then be set to 2. Since i is no longer 1, the else portion of the code at the top of the loop is executed. In this code, all individuals advance to the next age class, and moments later, we count the surviving females that make up the breeding population (1-year-olds on up). These breeders reproduce according to the birth rate, and we then allocate the offspring as males and females. These represent the 0-year-olds in the this time step, and the loop continues. Here we go . . .
Note: make sure to copy the entire script here and paste it in one fell-swoop. The most common error is a missing curly brace. If you are getting an error, check for matching braces. Don’t forget that you can click just to the left of an opening brace or bracket, and RStudio should highlight the matching bracket or brace.
# reset the pop array for a clean start
pop[,,,] <- 0
# set the stochastic settings
stoch.harvest <- FALSE
# set a random number seed for reproducibility
set.seed(4242)
# begin loop
for (i in 1:10) {
# Step 1. Population Census
if (i == 1) {
# Initialize the population seed for year 1
pop[1, age = , sex = 'f', stage = 'census'] <- female.seed
pop[1, age = , sex = 'm', stage = 'census'] <- male.seed
} else {
# advance individuals in previous year to the next age class.
pop[yr = i, age = 2:6, , stage = 'census'] <- pop[(i - 1), age = 1:5, , 'survivors']
# create 0 year olds
breeders <- pop[yr = i, age = 2:6, "f", stage = 'census']
birth.rates <- rates[yr = i, age = 2:6, "f", "birth"]
births <- round(breeders * birth.rates)
# allocate offspring by sex
male.offspring <- qbinom(p = 0.5, size = births, prob = 0.5)
female.offspring <- births - male.offspring
# add to pop array
pop[yr = i, age = 1 , sex = 'f', stage = 'census'] <- sum(female.offspring)
pop[yr = i, age = 1, sex = 'm', stage = 'census'] <- sum(male.offspring)
} # end of not i = 1
# Step 2. Harvest -----------------------------------
if (stoch.harvest == TRUE) {
# female harvest
pop[yr, age = , sex = "f", stage = "harvest"] <- rbinom(n = rep(1, times = 6),
size = pop[yr = i, age = , sex = "f", stage = "census"],
prob = rates[yr = i, age = , sex = "f", rate = "harvest"])
# male harvest
pop[yr = i, age = , sex = "m", stage = "harvest"] <- rbinom(n = rep(1, times = 6),
size = pop[yr = i, age = , sex = "m", stage = "census"],
prob = rates[yr = i, age = , sex = "m", rate = "harvest"])
} else {
# female harvest
pop[yr = i, age = , sex = "f", stage = "harvest"] <- qbinom(p = 0.5,
size = pop[yr = i, age = , sex = "f", stage = "census"],
prob = rates[yr = i, age = , sex = "f", rate = "harvest"])
# male harvest
pop[yr = i, age = , sex = "m", stage = "harvest"] <- qbinom(p = 0.5,
size = pop[yr = i, age = , sex = "m", stage = "census"],
prob = rates[yr = i, age = , sex = "m", rate = "harvest"])
} # end if
# Step 3. Escapees ---------------------------------
pop[yr = i, , "f","escapees"] <- pop[yr = i, , "f", "census"] - pop[yr = i, , "f", "harvest"]
pop[yr = i, , "m","escapees"] <- pop[yr = i, , "m", "census"] - pop[yr = i, , "m", "harvest"]
# Step 4. Survivors -----------------
# female survivors
pop[yr = i, age = , sex = "f", stage = "survivors"] <- qbinom(p = 0.5,
size = pop[yr = i, age = , sex = "f", stage = "escapees"],
prob = rates[yr = i, age = , sex = "f",rate = "survival"])
# male survivors
pop[yr = i, age = , sex = "m", stage = "survivors"] <- qbinom(p = 0.5,
size = pop[yr = i, age = , sex = "m", stage = "escapees"],
prob = rates[yr = i, age = , sex = "m",rate = "survival"])
} # end of year loopAnd now we can look at the results of the 10-year simulation, focusing on the population census:
## , , sex = f
##
## age
## yr 0 1 2 3 4 5
## 1 3000 1500 500 300 100 50
## 2 3010 1200 840 320 216 72
## 3 3201 1204 672 538 231 156
## 4 3356 1280 674 431 388 167
## 5 3516 1342 717 431 311 280
## 6 3589 1406 752 459 311 224
## 7 3717 1436 788 482 330 224
## 8 3856 1487 804 505 348 238
## 9 3996 1542 833 515 364 251
## 10 4138 1598 864 534 371 262
##
## , , sex = m
##
## age
## yr 0 1 2 3 4 5
## 1 1200 900 300 180 60 30
## 2 3010 480 441 168 114 38
## 3 3200 1204 235 247 106 72
## 4 3355 1280 590 132 156 67
## 5 3516 1342 627 331 83 98
## 6 3589 1406 657 351 209 52
## 7 3715 1436 689 368 222 132
## 8 3855 1486 704 386 232 140
## 9 3996 1542 728 395 243 146
## 10 4136 1598 755 408 249 15313.7 Converting Arrays to Dataframes
It’s useful to turn our results into a data frame for graphing. Plus, don’t forget that our ultimate goal is to create the harvest.csv file that we downloaded from the web. We have the basic dataset, but now we need to add additional information to it, and add some mistakes (typos) to it as well.
First, let’s convert the array to a dataframe with the spread function in the package, tidyr. This package is part of the tidyerse, an “opinionated collection of R packages designed for data science.” This function, and others in tidyr, allow a user to reshape the data in one R object into a different shape. Let’s load the package and then scan the helpfile.
Three of arguments to the spread function are required:
## function (data, key, value, fill = NA, convert = FALSE, drop = TRUE,
## sep = NULL)
## NULLFor the first argument, you pass in some data. The second argument, key is how you’d like to pivot the array. We would like to collapse the array into a dataframe, such that each entry in the arrays “stage” element is returned with a frequency by year, age, and sex. Let’s try it:
data <- tidyr::spread(as.data.frame.table(pop), key = stage, value = Freq)
# look at the structure of the returned data
str(data)## 'data.frame': 120 obs. of 7 variables:
## $ yr : Factor w/ 10 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ age : Factor w/ 6 levels "0","1","2","3",..: 1 1 2 2 3 3 4 4 5 5 ...
## $ sex : Factor w/ 2 levels "f","m": 1 2 1 2 1 2 1 2 1 2 ...
## $ census : num 3000 1200 1500 900 500 300 300 180 100 60 ...
## $ harvest : num 0 0 300 270 100 90 60 54 20 18 ...
## $ escapees : num 3000 1200 1200 630 400 210 240 126 80 42 ...
## $ survivors: num 1200 480 840 441 320 168 216 114 72 38 ...## yr age sex census harvest escapees survivors
## 1 1 0 f 3000 0 3000 1200
## 2 1 0 m 1200 0 1200 480
## 3 1 1 f 1500 300 1200 840
## 4 1 1 m 900 270 630 441
## 5 1 2 f 500 100 400 320
## 6 1 2 m 300 90 210 168
## 7 1 3 f 300 60 240 216
## 8 1 3 m 180 54 126 114
## 9 1 4 f 100 20 80 72
## 10 1 4 m 60 18 42 38See if you can match these values up with the pop array results, and confirm the data are correct. Notice that the column, yr is now a factor. We’ll want to convert these to integers for plotting:
Now that we have a dataframe, we can easily plot our Tauntaun population size through time:
library(ggplot2)
# fix this
ggplot(data, aes(x = yr, y = census, group = age)) +
geom_line(aes(linetype = age)) +
theme_minimal()
What’s the benefit of simulating the full population cycle for Tauntauns? Well, in previous chapters, you created a summary of the Tauntaun harvest with markdown, and created the SAK function to estimate population size and look at trends. By simulating a population, you can directly compare your estimated results (from the SAK function) with the true, simulated population. Simulation also allows you to use your population model as if it were an experiment; you can learn a lot by tweaking inputs and exploring how the dynamics change. In this exercise, you can add “noise” to the data by setting the harvest stochasticity settings to TRUE.
Now, there are many, many different ways we could have coded this model, and you will undoubtedly find your own coding style.
Our next steps will be to take the reported animals and masterfully create two csv files that provide information on each harvested animal, along with a hunter dataset. Before we do that, let’s have another break!

Figure 13.6: Time for another break!
13.8 Creating the Tauntaun Harvest Data CSV File
The Tauntaun biologist will not have access to the true population data. The only “glimpse” they have is the actual, reported harvest - information about a pile of dead Tauntauns. In this section, we’ll shape the harvest data into the csv file that you worked with in Chapters 6-8. This includes adding additional information about each harvested animal (such as fur color), and the town in which the animal was harvested. To add the town, we’ll dig into the spatial shapefile that contains the towns of Vermont (stored in your directory called towns), and then extract the shapefile’s attribute table. We’ll also add some mistakes to the data (because you almost never will have a perfectly proofed dataset before you analyze the data).
We’ll also simulate a hunter dataset (another csv file) that contains information about the person who harvested each reported animal (Han Solo is not on this list . . . a poacher!).
If you’ve had a break, you might need a reminder of our simulation outputs, now stored as a dataframe. Let’s have a look:
## 'data.frame': 120 obs. of 7 variables:
## $ yr : int 1 1 1 1 1 1 1 1 1 1 ...
## $ age : Factor w/ 6 levels "0","1","2","3",..: 1 1 2 2 3 3 4 4 5 5 ...
## $ sex : Factor w/ 2 levels "f","m": 1 2 1 2 1 2 1 2 1 2 ...
## $ census : num 3000 1200 1500 900 500 300 300 180 100 60 ...
## $ harvest : num 0 0 300 270 100 90 60 54 20 18 ...
## $ escapees : num 3000 1200 1200 630 400 210 240 126 80 42 ...
## $ survivors: num 1200 480 840 441 320 168 216 114 72 38 ...## yr age sex census harvest escapees survivors
## 1 1 0 f 3000 0 3000 1200
## 2 1 0 m 1200 0 1200 480
## 3 1 1 f 1500 300 1200 840
## 4 1 1 m 900 270 630 441
## 5 1 2 f 500 100 400 32013.8.1 Trimming Columns
The harvest data are stored in the column called “harvest”. We don’t need other columns such as “escapees” or “survivors”. Let’s trim these columns out now:
## yr age sex harvest
## 1 1 0 f 0
## 2 1 0 m 0
## 3 1 1 f 300
## 4 1 1 m 270
## 5 1 2 f 100
## 6 1 2 m 9013.8.2 Expanding the Dataframe Rows
This looks more like a harvest dataset. However, the harvest data normally won’t be recorded in this summarized format. Usually, each new harvested Tauntaun is added to the dataset, one record at a time. So we need to develop a record (row) for each harvested individual.
The number of individuals for each year is identified in the column ‘harvest’; we need a function that goes down the harvest vector row-by-row, replicating each row the number of times listed in the ‘harvest’ column.
For instance, our third record shows that 300 f individuals were harvested in year 1 that were 1 years old. We need to expand our grid so that each of the 300 individuals is stored on a unique row in the dataset.
The rep function does this (plus it can also be used to repeat elements of a vector). What we’ll do is first look at the row names of our data frame, and then we’ll repeat each row name by the number of animals harvested.
When used to repeat rows of a data frame, rep illustrates that the row name in a dataframe can actually reference the contents of the row.
# get the row names and store as a vector called rows
rows <- row.names(data)
# create a new vector called new.rows
# this repeats the elements within rows by the number of time stored in the harvest column
new.rows <- rep(rows, times = data$harvest)
# now put it all together
data <- data[rep(row.names(data), data$harvest), 1:3]
# look at the first five records
head(data)## yr age sex
## 3 1 1 f
## 3.1 1 1 f
## 3.2 1 1 f
## 3.3 1 1 f
## 3.4 1 1 f
## 3.5 1 1 fNotice that after we run rep, the row names are automatically changed so they remain unique (e.g., 3, 3.1 ,3.2, 3.3, etc). What is shown are some of the expanded Tauntauns from row 3 of our original data. In row 3, the original data noted that there were 300 harvested animals, you’re looking at the first 6 of these individuals. What happened to rows 1 and 2 in the original dataset? Well, since no Tauntauns of age class 0 were harvested, this information is omitted.
We will reassign integer-looking row names for visual clarity (but remember that R stores all row and column names as characters). First, we use the nrow function to count the number of rows in the table, and the colon operator to establish an integer sequence from 1 to the total number of rows. Then, we use the row.names function to assign row names with this sequence.
Now, we’ll create a new column called ‘individul’ which takes on the new row name. This is a typo that will need to be fixed in chapter 6. You’ll notice that the row names are characters, and although there is nothing wrong with this, we’ll use the as.numeric function to create unique numbers for each harvest record.
# create new column called "individul" (a typo)
data['individul'] <- as.numeric(row.names(data))
# peek at the records again
head(data)## yr age sex individul
## 1 1 1 f 1
## 2 1 1 f 2
## 3 1 1 f 3
## 4 1 1 f 4
## 5 1 1 f 5
## 6 1 1 f 6Converting the unique row names to integer-like characters is for more than just visual clarity. We’ve created a new column that uniquely identifies each individual, so that this column acts like a “primary key” for those of you familiar with databases.
Now, our Tauntaun harvest dataset is starting to look more like the way a Tauntaun biologist would normally see it. In the next section, we’ll add more columns of information for each harvest record.
13.8.3 Adding New Columns To A Data Frame
The first new column we’ll add to our data is a column called species, and we’ll populate it with the word “tauntaun”.
# A new column can also be added by naming it and supplying a single value for all rows
data['species'] <- 'tauntaun'Next, let’s introduce a few typos into this column so that we can practice repairing them in Chapter 6. Here, we randomly add a couple of misspelled species names into an otherwise uniform field.
This will let us use the sample function. The sample function has four arguments; here we’ll use three. The first argument, x, defines the samples you can draw from. The argument size is the number of samples you want. The argument, replace indicates whether you want to sample with replacement or not. Notice the default is FALSE, so if you don’t specify this argument, you will sample without replacement (which means you can’t have duplicates in your sample).
## function (x, size, replace = FALSE, prob = NULL)
## NULL# sample 14 rows between 1 and nrow without replacement; store as indices1
(indices1 <- sample(1:nrow(data), size = 14, replace = FALSE))## [1] 6404 11057 13290 12093 4667 11052 10602 8791 10660 3972 1597 4755 2903 13296# sample of 20 rows between 1 and nrows without replacement; store as indices2
(indices2 <- sample(1:nrow(data), size = 20, replace = FALSE))## [1] 12969 11333 8616 5630 11289 10036 8235 12256 5531 8988 11630 11010 2476 1331 13034 2277 7569 12352 12546 7340What exactly was returned? Well, the object named indices1 has a length of 14. It is 14 randomly sampled row numbers from our harvest dataset. the object named indices2 has a length of 20. It is 20 randomly sampled rows from our harvest dataset. We’ll make use of these two objects next:
# introduce a typo in the spelling of tauntaun for the randomly selected rows
data[indices1, 'species'] <- "tantaun"
data[indices2, 'species'] <- "tauntaan"Here, we replaced the value stored in data[indices1, ‘species’] with a typo, “tantaun”. The rows are provided by the indices1 object, and the column is the species column.
We’ll continue to add more attributes to the harvest dataset, including the “id” number of the hunter. We’ll create a new column called hunter.id. So, hunter.id of 1 points to hunter number 1 in the hunter dataset (which we’ll create in a few minutes). Here, we’ll create a new column in data called hunter.id, and assign a value to each record by sampling between 1 and hunters. In this case, we’ll set the replace argument to TRUE so that hunters can harvest more than one Tauntaun.
# assign the total number of known tauntaun hunters
hunters <- 700
# add a column called hunter.id to the data
data['hunter.id'] <- sample(1:hunters, size = nrow(data), replace = TRUE)
# look at the heading of the data
head(data)## yr age sex individul species hunter.id
## 1 1 1 f 1 tauntaun 285
## 2 1 1 f 2 tauntaun 56
## 3 1 1 f 3 tauntaun 549
## 4 1 1 f 4 tauntaun 296
## 5 1 1 f 5 tauntaun 521
## 6 1 1 f 6 tauntaun 355Next, we’ll add the date of harvest to our dataset. We’ll assume the legal harvest occurs in the months of October, November, and December. As you know, these have month numbers of 10, 11, and 12. We’ll use the sample function to randomly assign each Tauntaun harvest to one of these months. This time, we’ll include the argument called prob so that we can sample according to the monthly probabilities.
# add a field named 'month'
data['month'] <- sample(c(10, 11, 12), nrow(data), replace = TRUE, prob = c(0.5, 0.3, 0.2) )
# look at the first six records
head(data)## yr age sex individul species hunter.id month
## 1 1 1 f 1 tauntaun 285 10
## 2 1 1 f 2 tauntaun 56 11
## 3 1 1 f 3 tauntaun 549 12
## 4 1 1 f 4 tauntaun 296 12
## 5 1 1 f 5 tauntaun 521 11
## 6 1 1 f 6 tauntaun 355 1013.8.4 The “ifelse” Function
To insert day of the month is a little trickier, since not all months have the same number of days. Fortunately, both October and December have 31 days, leaving only November with 30. For simplicity we first populate the ‘day’ column with NAs. Then, we can use an ifelse function to work through the day column and replace the NA with a randomly sampled day between 1 and 30 (for November) or with a randomly sampled day between 1 and 31 (for October and December).
This is the first time we’ve used the ifelse function, so let’s take a moment to discuss it. If you check out the helpfile, you’ll see that “ifelse returns a value with the same shape as test which is filled with elements selected from either yes or no depending on whether the element of test is TRUE or FALSE.” This works a lot like Excel’s IF function. The first argument must be a logical test (something where the answer is TRUE or FALSE). The second argument specifies what to do if the answer is TRUE. The third argument specifies what to do if the answer evaluates to FALSE.
In the code below, we first set up a column called ‘day’ and populate it with NA’s. Then we use the ifelse function. The logical test is month == “November” (really, month == 11). If the month column indeed is November, then we carry out the second argument, which is collect random samples between 1 and 30 for each record where month == “November”. If the month column is not November, we just return the day column.
In this code, we’ll use another new function, with. This useful function helps you clean up your code to make it a bit more readable. The with function starts with the word with, followed by an open parenthesis, followed by an argument which is the object to work on (in our case, data). Then you add any additional code that involves the object. Finally, you close the with function with a closing parenthesis. When you specify “data” as the object to work on, you no longer need to use the dollar sign referencing because R already knows the object you’re working on . . . you’re free to write month instead of data$month, which some coders think is easier to read.
# make and name the column
data['day'] <- NA
#use the ifelse function to draw random samples between 1:30 if the month is November
data$day <- with(data, ifelse(month == 11,
yes = sample(1:30, size = sum(month == 11), replace = TRUE),
no = day))
#look at the data
head(data)## yr age sex individul species hunter.id month day
## 1 1 1 f 1 tauntaun 285 10 NA
## 2 1 1 f 2 tauntaun 56 11 13
## 3 1 1 f 3 tauntaun 549 12 NA
## 4 1 1 f 4 tauntaun 296 12 NA
## 5 1 1 f 5 tauntaun 521 11 21
## 6 1 1 f 6 tauntaun 355 10 NAThat takes care of November. What about day of harvest during October or December? We can use another ifelse function; this time our logical test will evaluate if the month is 10 or 12:
# draw random samples between 1:31 for month == 10 or month == 12
data$day <- with(data, ifelse(test = month == 10 | month == 12,
yes = sample(1:31, size = sum(month == 10 | month == 12),
replace = TRUE),
no = day))You may be wondering what the difference is between the ifelse function and the if notation for carrying out R code. In short, ifelse is an actual function, whereas if (test) { do something } else { do something else } is not. The if approach is generally used to control the flow of code (if something is true, jump to this bit of code, otherwise jump to that bit of code).
Now we have a familiar looking date, but it is spread across the three columns of month,day, and year. However, our year column doesn’t look much like a year that we know of (unless we are harvesting Tauntauns at the beginning of the common era). Let’s change the year column now by adding a constant to it:
Now then. To create a date for Chapter 6 readers, we need to combine the different fields using paste. This function combines a group of distinct values or objects into a single character vector much like the ‘concatenate’ function in Excel. This is a very useful function. Don’t forget Russell Crow, here. We want to apply this function to all rows, and specify the column names in our paste function.
# create a date character string with the paste function
data['date'] <- paste(data[,'month'],data[,'day'],data[,'yr'], sep = "/")
# look at the structure of data
str(data)## 'data.frame': 13351 obs. of 9 variables:
## $ yr : num 1901 1901 1901 1901 1901 ...
## $ age : Factor w/ 6 levels "0","1","2","3",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ sex : Factor w/ 2 levels "f","m": 1 1 1 1 1 1 1 1 1 1 ...
## $ individul: num 1 2 3 4 5 6 7 8 9 10 ...
## $ species : chr "tauntaun" "tauntaun" "tauntaun" "tauntaun" ...
## $ hunter.id: int 285 56 549 296 521 355 674 297 7 388 ...
## $ month : num 10 11 12 12 11 10 11 10 11 12 ...
## $ day : int 8 13 26 11 21 18 4 4 18 14 ...
## $ date : chr "10/8/1901" "11/13/1901" "12/26/1901" "12/11/1901" ...That looks more like a typical date entry.
13.8.5 Adding Towns from Shapefile Attributed Table
Next, we will add in the town in which each record of the harvest table originates. We worked with a town shapefile in Chapter 7, which is stored in the towns directory. As you know, shapefiles consist of multiple files that have the same filename, but have different extensions. Shapefiles consist of many files sharing the same core filename and different suffixes (i.e. file extensions). For example, the town shapefile consists of the following files:
## [1] "towns.zip" "VT_Data_-_Town_Boundaries.cpg" "VT_Data_-_Town_Boundaries.dbf" "VT_Data_-_Town_Boundaries.prj"
## [5] "VT_Data_-_Town_Boundaries.shp" "VT_Data_-_Town_Boundaries.shx" "VT_Data_-_Town_Boundaries.xml"The package rgdal can be used to work with such files. We can use the readOGR function to read this shapefile into R. The attribute table is stored in the “data” slot.
# load the package rgdal
library(rgdal)
# use the st_read function to read in the shapefile
towns <- readOGR(dsn = "towns", layer = "VT_Data_-_Town_Boundaries")## OGR data source with driver: ESRI Shapefile
## Source: "C:\Users\tdonovan\University of Vermont\Spreadsheet Project - General\R Training\Fledglings\towns", layer: "VT_Data_-_Town_Boundaries"
## with 255 features
## It has 8 fields## Formal class 'SpatialPolygonsDataFrame' [package "sp"] with 5 slotsAs you can see, this is an object of class ‘SpatialPolygonsDataFrame’ from the package, “sp”. This is an S4 object that is deeply structured (we’re only looking at the top level). The information in S4 objects are stored in “slots”, which can be accessed with the @ symbol. Let’s plot this shapefile so you can see what’s what:

And now, let’s look at the attribute table, which is stored in the data slot.
## OBJECTID FIPS6 TOWNNAME TOWNNAMEMC CNTY TOWNGEOID ShapeSTAre ShapeSTLen
## 0 1 9030 CANAAN Canaan 9 5000911800 86133926 63085.37
## 1 2 11040 FRANKLIN Franklin 11 5001127100 105502442 42582.92
## 2 3 11015 BERKSHIRE Berkshire 11 5001105425 108509286 41941.76
## 3 4 11050 HIGHGATE Highgate 11 5001133025 155573562 57367.84
## 4 5 11060 RICHFORD Richford 11 5001159125 111897347 42398.62
## 5 6 13005 ALBURGH Alburgh 13 5001300860 123041223 55791.54
## 6 7 9080 NORTON Norton 9 5000952750 100482148 43902.68
## 7 8 9005 AVERILL Averill 9 5000902125 98589185 39794.77
## 8 9 19050 HOLLAND Holland 19 5001933775 100189636 40818.36
## 9 10 19060 JAY Jay 19 5001936325 87962933 37738.29See the column named TOWNNAME? This single column in the attributes table contains the towns in Vermont. Let’s use the sample function once more to assign a town of harvest to each and every Tauntaun in our dataset.
# convert a single field in the data frame to a character vector of town names
towns <- towns@data$TOWNNAME
# create a town field and populate it with random value from the town name vector
data$town <- sample(towns, nrow(data), replace = TRUE)
# look at the first 10 records of data
head(data, n = 10)## yr age sex individul species hunter.id month day date town
## 1 1901 1 f 1 tauntaun 285 10 8 10/8/1901 STANNARD
## 2 1901 1 f 2 tauntaun 56 11 13 11/13/1901 BALTIMORE
## 3 1901 1 f 3 tauntaun 549 12 26 12/26/1901 HANCOCK
## 4 1901 1 f 4 tauntaun 296 12 11 12/11/1901 ST. ALBANS TOWN
## 5 1901 1 f 5 tauntaun 521 11 21 11/21/1901 WHEELOCK
## 6 1901 1 f 6 tauntaun 355 10 18 10/18/1901 PEACHAM
## 7 1901 1 f 7 tauntaun 674 11 4 11/4/1901 AVERYS GORE
## 8 1901 1 f 8 tauntaun 297 10 4 10/4/1901 SUDBURY
## 9 1901 1 f 9 tauntaun 7 11 18 11/18/1901 MOUNT HOLLY
## 10 1901 1 f 10 tauntaun 388 12 14 12/14/1901 BROOKFIELDNow we know who harvested each Tauntaun, on what day, and in which town. Notice that R thinks that “town” is a factor with 255 levels. That’s fine.
13.8.6 The Normal Distribution
Let’s continue to add more variables to the harvest dataset, focusing on adding different kinds of datatypes. Let’s start by adding some numeric (decimal) data types. Each Tauntaun will have a length; males will be longer than females. We’ll use another probability distribution, the normal distribution to assign lengths. No doubt, you’ve encountered this distribution before. The shape of the normal distribution is controlled by two parameters, the mean and the standard deviation. We can create a normal distribution with thednorm function. These arguments are called mean and sd. For example, let’s look at a normal distribution whose mean is 50 and whose standard deviation is 10:
# use `dnorm` to return the probability of observing x, given the mean and standard deviation
probs <- dnorm(x = 1:100, mean = 50, sd = 10)
# plot x along the axis, and probs along the y axis.
plot(x = 1:100, y = probs,
type = "l",
xlab = "X",
ylab = "probability",
main = "Normal Distribution")
Notice how this distribution is centered on 50? If we draw random samples from this distribution, you can see that it is much more likely to draw samples near 50 than samples in the tails of the distribution.
We can use the rnorm function to draw samples from a normal distribution. Like rbinom and we can specify how many samples to draw with the n argument. Note that this function has a default mean of 0 and a default sd of 1 (a Z score), so we must set these arguments or R will use the defaults.
In the code below, we use different means for males and females,so we need to subset data to include only those rows where sex == ‘m’ or sex ==‘f’. To do that subset, we use rnorm and draw the number of samples within the subset from a normal distribution with a specified mean and standard deviation. We used the ifelse function once again, following the same logic as we did when assigning the day of harvest. You should be able to work through the arguments.
## function (n, mean = 0, sd = 1)
## NULL# add a column called length
data$length <- NA
# add lengths of harvested animals (males)
data$length <- with(data,
ifelse(sex == "m",
round(rnorm(n = nrow(data['sex' == 'm']),
mean = 400,
sd = 40),2),
length))
# add lengths of harvested animals (females)
data$length <- with(data,
ifelse(sex == "f",
round(rnorm(n = nrow(data['sex' == 'f']),
mean = 300,
sd = 20),2),
length))
# look the first few records
head(data,3)## yr age sex individul species hunter.id month day date town length
## 1 1901 1 f 1 tauntaun 285 10 8 10/8/1901 STANNARD 277.10
## 2 1901 1 f 2 tauntaun 56 11 13 11/13/1901 BALTIMORE 311.86
## 3 1901 1 f 3 tauntaun 549 12 26 12/26/1901 HANCOCK 274.84Next, we’ll add a new column called weight, which is the weight of harvested animals in some Jedi metric (integer data). Here, we’ll assume that weight is correlated with an animals length.
The fastest way to create correlated weight data is to establish a linear relationship between length and weight, and add some noise to this relationship. Let’s run some code, and then discuss it.
# create column called weight, which is the length * 2.5
data$weight <- data$length * 2.5
# add noise to the weight column by adding a random deviate generated by rnorm
data$weight <- data$weight + rnorm(n = nrow(data), mean = 0, sd = 100)
# look at the data
head(data)## yr age sex individul species hunter.id month day date town length weight
## 1 1901 1 f 1 tauntaun 285 10 8 10/8/1901 STANNARD 277.10 699.3044
## 2 1901 1 f 2 tauntaun 56 11 13 11/13/1901 BALTIMORE 311.86 718.1022
## 3 1901 1 f 3 tauntaun 549 12 26 12/26/1901 HANCOCK 274.84 550.6420
## 4 1901 1 f 4 tauntaun 296 12 11 12/11/1901 ST. ALBANS TOWN 266.70 699.5951
## 5 1901 1 f 5 tauntaun 521 11 21 11/21/1901 WHEELOCK 271.84 613.3350
## 6 1901 1 f 6 tauntaun 355 10 18 10/18/1901 PEACHAM 301.03 851.4671Next, let’s double check the correlation between length and weight – this is done so that the fledgling cor function in the chapter on statistical analysis:
## [1] 0.8287147# visualize the data
plot(x = data$length,
y = data$weight,
main = "Scatterplot Example",
xlab = "Length ",
ylab = "Weight ",
pch = 19) 
# check the correlation for males and females separately
males <- subset(data, sex == 'm')
cor(males$weight, males$length)## [1] 0.7093369## [1] 0.7093369Here, we’ve multiplied each Tauntaun’s length by 2.5 to give us each animal’s weight. Then, we used the rnorm function again, this time drawing random values from a distribution whose mean is 0 and whose standard deviation is 100. These deviates were then added to the vector of weights to give us our final weights. The standard deviation argument controls how much “noise” we added to the data. We then subset the males and females, and used the cor function to double-check how correlated height and weight are for males and females. All of this was done so that a fledgling reader can lean how to use the cor function in the chapter on statistical analysis.
Now, let’s add in some outlier lengths so the Tauntaun biologist can practice finding outliers. We will create a random vector of rows that will be used for indexing, and we’ll store the index so we can extract the current lengths, multiply them by 10, and reinsert the new length in the right place.
# draw 6 random samples of row numbers from the data; these rows will contain outliers
bad.len <- sample(1:nrow(data), size = 6)
# multiply the original length by 10, and replace the outliers into the original dataset
data[bad.len,'length'] <- data[bad.len,'length'] * 10Heh, heh, heh.
13.8.7 Adding Factor-like Data
That takes care of a few columns with continuous data. Now let’s add some nominal data types (names, which are stored as characters). We’ll add the following columns: method of harvest and color of the Tauntaun’s fur. Again we’ll use the sample function to draw samples according to a probability vector . . . remember that your probabilities must sum to 1! Then we’ll introduce NA’s and typos.
# add method of harvest (nominal data)
data['method'] <- sample(c('muzzle','bow', 'lightsaber'),
size = nrow(data),
prob = c(0.25,0.25,0.50),
replace = TRUE)
# delete a few method records to spike the data with realistic errors
data[sample(1:nrow(data), size = 512), 'method'] <- NA
# add fur color (nominal data)
data['color'] <- sample(c('gray','white'),
size = nrow(data),
replace = TRUE,
prob = c(0.68,0.32))
# add some bad fur colors
bad.fur.indices <- sample(1:nrow(data), size = 1306)
data[bad.fur.indices,'color'] <- 'grey'Finally, we’ll add in one column that contains ordinal (or ordered) data. Let’s assume that Tauntauns have fur length that can be defined as “short”, “medium”, or “long”. Note that this is ordered data, but we don’t know how short is “short” or how short is “medium”. We only know that short < medium < long. This lets us work with ordered factors in Chapter 6.
# add fur length (ordinal, or ordered, data)
data['fur'] <- sample(c('short','medium','long'),
size = nrow(data), replace = TRUE)Nice! We now have all of the rows and variables (columns) of harvest data for our chapter 6 user.
13.8.8 Sorting (Ordering) Data Frames
Before we create a csv file from the data, let’s clean it up in terms of sorting the data and columns.
Sorting is a simple task that can be frustratingly tricky until you’ve seen it once or twice. Let’s sort the table in order of increasing individual ID, which is in the column ‘individual’. You’d think that sort would be the function of choice, but it’s not. The order function is used instead to allow us the option for sorting by multiple columns if we wish. With order, you simply enter each additional sort vector as an argument of the function separated by commas). Save sort for sorting vectors.
# sort the pop data by individul (a typo)
data <- data[order(data[,'individul']),]
# preview the table
head(data,10)## yr age sex individul species hunter.id month day date town length weight method color fur
## 1 1901 1 f 1 tauntaun 285 10 8 10/8/1901 STANNARD 277.10 699.3044 lightsaber white long
## 2 1901 1 f 2 tauntaun 56 11 13 11/13/1901 BALTIMORE 311.86 718.1022 muzzle gray long
## 3 1901 1 f 3 tauntaun 549 12 26 12/26/1901 HANCOCK 274.84 550.6420 bow white long
## 4 1901 1 f 4 tauntaun 296 12 11 12/11/1901 ST. ALBANS TOWN 266.70 699.5951 muzzle gray long
## 5 1901 1 f 5 tauntaun 521 11 21 11/21/1901 WHEELOCK 271.84 613.3350 bow gray long
## 6 1901 1 f 6 tauntaun 355 10 18 10/18/1901 PEACHAM 301.03 851.4671 lightsaber grey short
## 7 1901 1 f 7 tauntaun 674 11 4 11/4/1901 AVERYS GORE 256.77 720.2733 lightsaber white short
## 8 1901 1 f 8 tauntaun 297 10 4 10/4/1901 SUDBURY 306.25 579.1136 bow gray long
## 9 1901 1 f 9 tauntaun 7 11 18 11/18/1901 MOUNT HOLLY 317.58 842.1904 lightsaber white medium
## 10 1901 1 f 10 tauntaun 388 12 14 12/14/1901 BROOKFIELD 310.31 867.4912 lightsaber white longLooks good. But the columns might not be organized in a way that matches the Tauntaun harvest data collection form. To reorganize the columns within our dataset, just specify the columns in the order you’d like. Here, we’ll mix them up in the order that you, the Tauntaun biologist, will receive the dataset.
data <- data[,c("hunter.id", "age", "sex", "individul", "species", "date", "town", "length", "weight","method", "color", "fur")]Notice that we’ve left a few columns out (such as month, day, and year), which means they’ll be dropped.
13.8.9 Saving the Harvest CSV file
Finally, let’s save the complete simulated harvest recordset to the working directory as a comma separated values file with the write.csv function.
write.csv(data, file = 'datasets/TauntaunHarvest.csv', row.names = FALSE)
# confirm the file exists
file.exists("datasets/TauntaunHarvest.csv")## [1] TRUE13.8.10 The Hunter CSV file
In addition to the harvest dataset, we need a table that stores data pertaining to active hunters. Specifically we want to store their gender (in a character field as either ‘m’ or ‘f’), whether they are a state resident (in a logical field, either TRUE or FALSE), and we will assign each one a unique license number, which we will call their hunter ID. Again we will just use random values for each hunter, assigning them with sample according to predefined frequencies that we want to see in the resulting vectors. We could call sample for each vector, but to save a step this time we will nest multiple calls to sample inside the call to data.frame.
# create a dataset of hunter information.
hunter <- data.frame(hunter.id = 1:hunters,
sex.hunter = sample(c('m','f'),
size = hunters,
replace = TRUE,
prob = c(0.85, 0.15)),
resident = sample(c(TRUE,FALSE),
size = hunters,
replace = TRUE,
prob = c(0.8, 0.2)))
# look at the data
head(hunter)## hunter.id sex.hunter resident
## 1 1 m TRUE
## 2 2 m FALSE
## 3 3 m TRUE
## 4 4 m TRUE
## 5 5 m FALSE
## 6 6 f TRUE# Save the CSV file
write.csv(hunter,file = 'datasets/hunter.csv', row.names = FALSE)
# confirm the file exists
file.exists("datasets/hunter.csv")## [1] TRUEThat wraps up this chapter. Hopefully you now understand how we created the two csv files that you inherited as the new Tauntaun biologist, which include mistakes.
This has been a deep, deep chapter. We’ve learned a lot about arrays, rates, statistical distributions, loops, and more! If you have been thinking to yourself “I think I can code this a bit differently than what’s shown”, you’ve definitely caught the R bug. As we said in Chapter 1, you won’t learn R in 3 days. But, hopefully you have learned some tools that will help make your journey a bit easier from this point forward.
Most importantly, if you were able to follow along with this chapter, you’ve fledged!
Figure 13.7: Time for another break!