Hash collisions

Published

2023-08-05

The pigeonhole principle. Source: Wikipedia

As we have seen in previous videos, it happens sometimes that two keys yield the same hash value for a given table size. This is called a “hash collision” or just “collision.”

Why do hash collisions occur? What factors contribute to the frequency with which we expect collisions to occur? Again, as we’ve seen there are two factors and they are interrelated: table size and the hash function itself.

In the most extreme case regarding table size, say we had a table size of n and we wanted to insert n + 1 objects. Even if our hashing had been perfect up to the nth insertion—that is, there were no collisions when inserting the first n objects—we would necessarily have a collision when inserting the next object. In one sense, this seems so obvious as to hardly bear mentioning, but in fact this is an important concept in computer science and mathematics called the “pigeonhole principle.” Stated a little more formally, given n containers and m objects with m > n, then at least one container must contain more than one object. A canonical example is given thus: the maximum number of hairs on a human head is around 150,000, therefore in any city with population greater than 150,000 there must be at least two people (probably a lot more) that must have exactly the same number of hairs on their heads! That’s the pigeonhole principle.

One way to reduce the number of collisions is to increase the hash table size. The bigger the hash table, the less frequent are collisions. This is true, but we don’t want to make our hash tables too big—we could waste a lot of space! A general rule of thumb is that the size of our hash table should be between 1.3 times and 2.0 times the number of objects we wish to store. If it gets bigger than that, we’re wasting space. Obviously there’s a trade-off here: the smaller the table, the more frequent are collisions, and the bigger the table, the greater the risk of wasting space. An important metric is the so-called “load factor” (the textbook calls this “fill percentage”). Expressing the rule of thumb just given in terms of load factor, we want our load factor to be within the range 50% to 75%. Load factor of 50% occurs when our hash table size is twice the number of objects we wish to store. Load factor of 75% occurs when we have a hash table size that’s approximately 1.3 times the number of objects we wish to store.

The other factor that determines the frequency with which we expect collisions to occur is the hash function itself. Recall that the hash function takes some hashable object and returns a number modulo the size of the hash table. Generally, we think of the hash function proper as the function that calculates an number from its input before taking the modulus. This function should distribute values more-or-less uniformly—that is, values in its range should be equally likely. In this way, when we take the modulus, we’ll be less likely to have a collision. In an extreme case, let’s say are hash function always returned the same value, no matter what the input—then we’d have a collision every time! This is why we want the part of our hash function before taking the modulus to distribute values as uniformly as possible.

We’ve given the example of a simple Horner hash function, with x being some prime number. In this case, for an input string of n characters, we calculate a polynomia

Horner hash polynomial

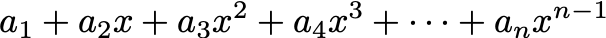
and we’ve seen this distributes values reasonably well.

There are other, more sophisticated hash functions which are outside the scope of this course. We’ll let Horner hash suffice for our purposes.

Keep in mind that in order to be useful, a hash function must be easy to compute. If a hash function takes too long to compute it defeats the purpose of hash tables which are meant to provide fast insertion, lookup, and removal.

In the language of mathematics, you may have heard the terms “one-to-one” or “injective,” and “onto” or “surjective.” If a function is one-to-one, it means that each element in its domain is mapped to a distinct element in its codomain. Onto means that each element in the codomain has at least one element in the domain that maps to it.

In our context, the domain of the hash function is the set of all possible keys, and the codomain is the set of valid indices into our hash table. We’ve seen that for hash functions (where we include taking the modulus of the table size) cannot be one-to-one —the pigeonhole principle proves this to be so. But we would like our hash functions to be onto. That is, we’d like our hash function to cover all the possible indices into our hash table. A hash function wouldn’t be very good if it could never yield a certain index. In that event, that element in our hash table could never be used!

In summary, no hash function is perfect, and our hash tables are always of some finite size—so collisions will occur. We wish to make these collisions as infrequent as reasonably possible, but we don’t want to expand the size of our hash table so that we waste a lot of space. There’s always a trade-off.

So collisions are a fact of life. The will occur. We are left with the problem of how to handle them when they do occur. This will be the subject of future lectures and demonstrations.

Supplemental reading:

Comprehension check:

True or false? Excluding trivial examples like a hash table with only one entry, no matter what we do, it is impossible to avoid collisions entirely.
Before taking the modulus we want our hash function to distribute values as _______________ as possible.
Chittenden County has a population of 164,000. The maximum number of hairs on a human head is 150,000. Therefore, there must be at least ________ people in Chittenden County with at least one other person having exactly the same number of hairs on their head.
If we have a hash table of size 100 storing 67 objects, its load factor is approximately __________.
As a rule of thumb, we want the size of our hash table to be between __________ and __________ times the number of objects we wish to store.

Answers: 0˙ᄅ / Ɛ˙Ɩ / %ㄥ9 / 000ㄣƖ / ʎlɯɹoɟᴉun / ǝnɹʇ

Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >

No generative AI was used in producing this material. This was written the old-fashioned way.