Euclid’s Algorithm (GCD)

An ancient algorithm with a while loop

There’s a rather beautiful algorithm for finding the greatest common divisor of two positive integers.

You may recall from your elementary algebra course that the greatest common divisor of two positive integers, a and b, is the greatest integer which divides both a and b without a remainder.

For example, the greatest common divisor of 120 and 105 is 15. It’s clear that 15 is a divisor of both 120 and 105:

\begin{align*} 120 / 15 &= 8 \\ 105 / 15 &= 7. \end{align*}

How do we know that 15 is the greatest common divisor? One way is to factor both numbers and find all the common factors.

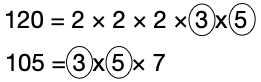
We’ve found the common factors of 120 and 105, which are 3 and 5, and their product is 15. Therefore, 15 is the greatest common divisor of 120 and 105. This works, and it may well be what you learned in elementary algebra, however, it becomes difficult with larger numbers and isn’t particularly efficient.

Euclid’s algorithm

Euclid was an ancient Greek mathematician who flourished around 300 BCE. Here’s an algorithm that bears Euclid’s name. It was presented in Euclid’s Elements, but it’s likely that it originated many years before Euclid.¹

Euclid’s GCD algorithm

Let’s work out an example. Say we have a = 342 and b = 186.

First, we find the remainder of 342 / 186. 186 goes into 342 once, leaving a remainder of 156. Now, let a = 186, and let b = 156. Does b equal 0? No, so we continue.

Find the remainder of 186 / 156. 156 goes into 186 once, leaving a remainder of 30. Now, let a = 156, and let b = 30. Does b equal 0? No, so we continue.

Find the remainder of 156 / 30. 30 goes into 156 five times, leaving a remainder of 6. Now, let a = 30, and let b = 6. Does b equal 0? No, so we continue.

Find the remainder of 30 / 6. 6 goes into 30 five times, leaving a remainder of 0. Now, let a = 6, and let b = 0. Does b equal 0? Yes, so we are done.

The GCD is the value of a, so the GCD is 6.

Pretty cool, huh?

Why does it work?

If we have a and b both positive integers, with a > b, then we can write

a = bq + r

where q is the quotient of dividing a by b (Euclidean division) and r is the remainder. For example, in the first step of our example (above) we have

342 = 1 \times 186 + 156.

It follows that the GCD of a and b equals the GCD of b and r. That is,

\text{gcd}(a, b) = \text{gcd}(b, r).

Thus, by successive divisions, we continue to reduce the problem to smaller and smaller terms. At some point in the execution of the algorithm, b becomes 0, and we can divide no further. At this point, what remains as the value for a is the GCD, because the greatest common divisor of a and zero is a!

This algorithm saves us from having to factor both terms.

Consider a larger problem instance with a = 30759 and b = 9126. Factoring these would be a nuisance, but the Euclidean algorithm takes only eight iterations to find the answer, 3.

Show me the code!

Here’s an implementation in Python.

"""
Implementation of Euclid's algorithm.
"""

a = int(input("Enter a positive integer, a: "))
b = int(input("Enter a positive integer, b: "))

while b != 0:
    remainder = a % b
    a = b
    b = remainder

print(f"The GCD is {a}.")

That’s one elegant little algorithm (and one of my personal favorites). It also demonstrates the use of a while loop, which is needed, since we don’t know a priori how many iterations it will take to reach a solution.

Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >

No generative AI was used in producing this material. This was written the old-fashioned way.

This material is for free use under either the GNU Free Documentation License or the Creative Commons Attribution-ShareAlike 3.0 United States License (take your pick).

Footnotes

1. Some historians believe that Eudoxus of Cnidus was aware of this algorithm (c. 375 BCE), and it’s quite possible it was known before that time.