Modulo, floor division, and modular arithmetic

Published

2023-08-02

Euclidean or “floor” division

When presenting expressions, we saw examples of common arithmetic operations: addition, subtraction, multiplication, and division. Here we will present two additional operations which are closely related: the modulo or “remainder” operator, and what’s variously called “quotient”, “floor division”, “integer division” or “Euclidean division.”1

Chances are, when you first learned division in primary school, you learned about Euclidean (floor) division. For example, 17 \div 5 = 3 \text{ r } 2, or 21 \div 4 = 5 \text{ r } 1. In the latter example, we’d call 21 the dividend, 4 the divisor, 5 the quotient, and 1 the remainder.

Obviously the operations of finding the quotient and the remainder are closely related. For any two integers a, b, with b \neq 0 there exist unique integers q and r such that

a = bq + r

where q is the Euclidean quotient and r is the remainder.

Furthermore, 0 \leq r < |b|, where |b| is the absolute value of b. This should be familiar.

Just in case you need a refresher:

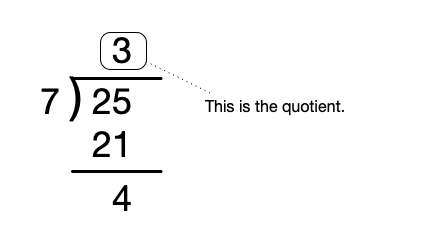
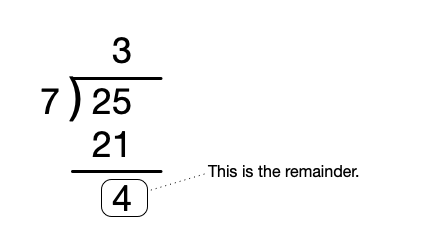
Python’s // and % operators

Python provides us with operators for calculating quotient and remainder. These are // and %, respectively. Here are some examples:

>>> 17 // 5  # calculate the quotient
3
>>> 17 % 5   # calculate the remainder
2
>>> 21 // 4  # calculate the quotient
5
>>> 21 % 4   # calculate the remainder
1

You may ask: What’s the difference between the division we saw earlier, /, and floor division with //? The difference is that / calculates the quotient as a decimal expansion. Here’s a simple comparison:

>>> 4 / 3
1.3333333333333333   # three goes into four 1 and 1/3 times
>>> 4 // 3           # calculates Euclidean quotient
1
>>> 4 % 3            # calculates remainder
1

Common questions

What happens when the divisor is zero?

Just as in mathematics, we cannot divide by zero in Python either. So all of these operations will fail if the right operand is zero, and Python will complain: ZeroDivisionError.

What happens if we supply floating-point operands to // or %?

In both cases, operands are first converted to a common type. So if one operand is a float and the other an int, the int will be implicitly converted to a float. Then the calculations behave as you’d expect.

>>> 7 // 2    # if both operands are ints, we get an int
3
>>> 7.0 // 2  # otherwise, we get a float...
3.0
>>> 7 // 2.0
3.0
>>> 7.0 // 2.0
3.0
>>> 7 % 2     # if both operands are ints, we get an int
1
>>> 7.0 % 2   # otherwise, we get a float...
1.0
>>> 7 % 2.0
1.0
>>> 7.0 % 2.0
1.0

What if the dividend is zero?

What are 0 // n and 0 % n?

>>> 0 // 5    # five goes into zero zero times
0
>>> 0 % 5     # the remainder is also zero
0

What if the dividend is less than the divisor?

What are m // n and m % n, when m < n, with m and n both integers, and m \geq 0, n > 0?

The first one’s easy: if m < n?, then m // n yields zero. The other trips some folks up at first.

>>> 5 % 7
5

That is, seven goes into five zero times and leaves a remainder of five. So if m < n, then m % n yields m.

What if the divisor is negative?

What is m % n, when n < 0? This might not work the way you’d expect at first.

>>> 15 // -5
-3
>>> 15 % -5
0

So far, so good. Now consider:

>>> 17 // -5
-4
>>> 17 % -5
-3

Why does 17 // -5 yield -4 and not -3? Remember that this is what’s called “floor division.” What Python does, is that it calculates the (floating-point) quotient and then applies the floor function.

The floor function is a mathematical function which, given some number x, returns the largest integer less than or equal to x. In mathematics this is written as:

\lfloor x \rfloor .

So in the case of 17 // -5, Python first converts the operands to float type, then calculates the (floating-point) quotient, which is -3.4 and then applies the floor function, to yield -4 (since -4 is the largest integer less than or equal to -3.4).

This also makes clear why 17 % -5 yields -3. This preserves the equality

\begin{align*} a &= bq + r \\ 17 &= (-5 \times -4) + (-3) \\ 17 &= 20 - 3. \end{align*}

What if the dividend is negative?

>>> -15 // 5
-3
>>> -15 % 5
0

So far so good. Now consider:

>>> -17 // 5
-4
>>> -17 % 5
3

Again, Python preserves the equality

\begin{align*} a &= bq + r \\ -17 &= (5 \times -4) + 3 \\ -17 &= -20 + 3. \end{align*}

Yeah. I know. These take a little getting used to.

What if dividend and divisor both are negative?

Let’s try it out—having seen the previous examples, this should come as no surprise.

>>> -43 // -3
14
>>> -43 % -3
-1

Check this result:

\begin{align*} a &= bq + r \\ -43 &= (-3 \times 14) + (-1) \\ -43 &= -42 - 1 \end{align*}

The % operator will always yield a result with the same sign as the second operand (or zero).

You are encouraged to experiment with the Python shell. It is a great tool to further your understanding.

Modular arithmetic

Now, in the Python documentation2, you’ll see // referred to as floor division. You’ll also see that % is referred to as the modulo operator.

It’s fine to think about % as the remainder operator (with the provisos noted above), but what is a “modulo operator”?

Let’s start with the example of clocks.

Figure 1: Clock face

Perhaps you don’t realize it, but you do modular arithmetic in your head all the time. For example, if you were asked what time is 5 hours after 9 o’clock, you’d answer 2 o’clock. You wouldn’t say 14 o’clock.3 This is an example of modular arithmetic. In fact, modular arithmetic is sometimes called “clock arithmetic.”

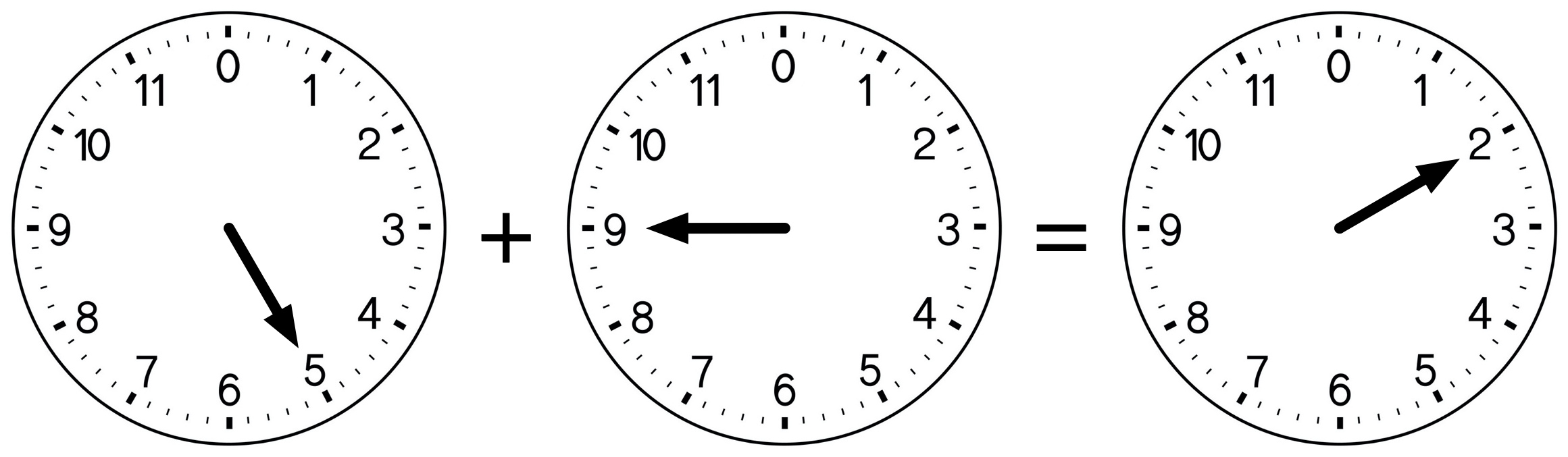
Figure 2: Clock arithmetic: 5 + 9 \equiv 2 \pmod {12}

In mathematics, we would say that 5 + 9 is congruent to 2 modulo 12, and we’d write

5 + 9 \equiv 2 \pmod {12}

So 5 + 9 = 14 and 14 ÷ 12 has a remainder of 2.

Here’s another example:

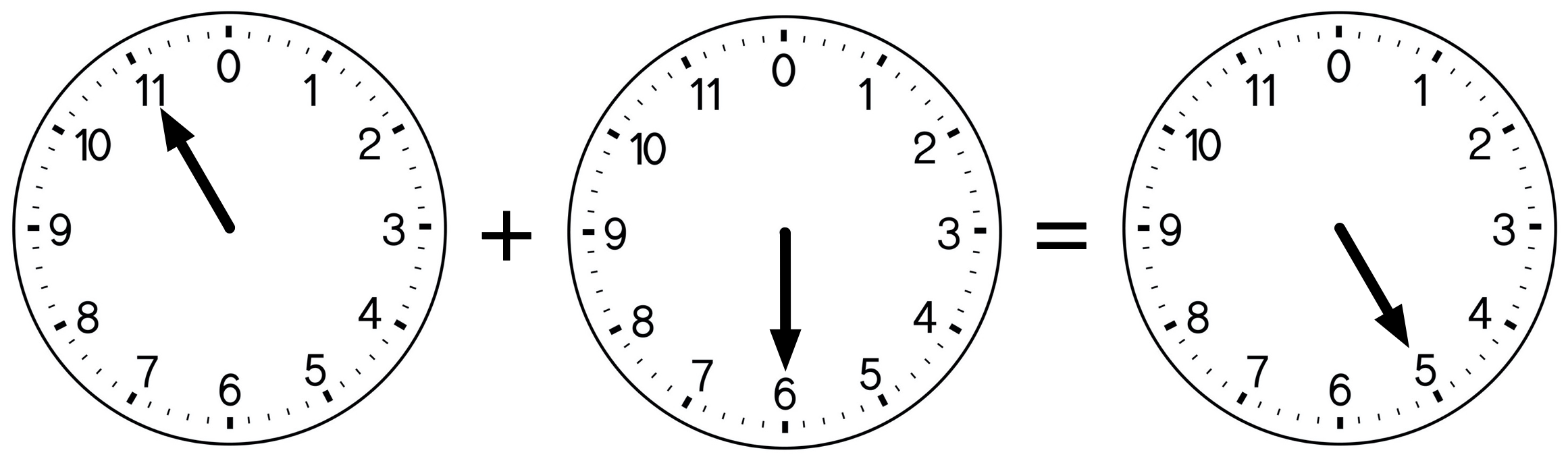
Figure 3: Clock arithmetic: 11 + 6 \equiv 5 \pmod {12}

Similarly, we’d say that 11 + 6 is congruent to 5 modulo 12, and we’d write

11 + 6 \equiv 5 \pmod {12}

Let’s think of this a little more formally. Suppose we have some positive integer, n, which we call the modulus. We can perform arithmetic with respect to this integer in the following way. When counting, when we reach this number we start over at 0. Now in the case of clocks, this positive integer is 12, but it needn’t be—we could choose any positive integer.

For example, with n = 5, we’d count

0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, \ldots

Notice that we never count to 5, we start over at zero. You’ll see that the clocks in the figures above don’t have twelve on their face but instead have zero. If n = 5, then we’d have 5 positions on our “clock”, numbered 0 through 4.

Figure 4: A “clock” for (mod 5)

Under such a system, addition and subtraction would take on a new meaning. For example, with n = 5, 4 + 1 \equiv 0 \pmod 5,

Figure 5: 4 + 1 \equiv 0 \pmod 5

4 + 2 \equiv 1 \pmod 5,

Figure 6: 4 + 2 \equiv 1 \pmod 5

4 + 3 \equiv 2 \pmod 5,

Figure 7: 4 + 3 \equiv 2 \pmod 5

and so on.

Things work similarly for subtraction, except we proceed anti-clockwise. For example 1 - 3 \equiv 3 \pmod 5.

Figure 8: 1 - 3 \equiv 3 \pmod 5

The same principle applies to multiplication: 2 \times 4 \equiv 3 \pmod 5 and 3 \times 3 \equiv 4 \pmod 5.

Negative modulus

We’ve seen that when we add we go clockwise, and when we subtract we go anti-clockwise. What happens when the modulus is negative?

To preserve the “direction” of addition (clockwise) and subtraction (anti-clockwise), if our modulus is negative we number the face of the clock anti-clockwise.

Figure 9: A “clock” for (mod -5)

Examples:

1 \equiv -4 \pmod{-5}

Figure 10: 1 \equiv -4 \pmod {-5}

2 \equiv -3 \pmod{-5}

Figure 11: 2 \equiv -3 \pmod {-5}

2 + 4 \equiv -4 \pmod{-5}

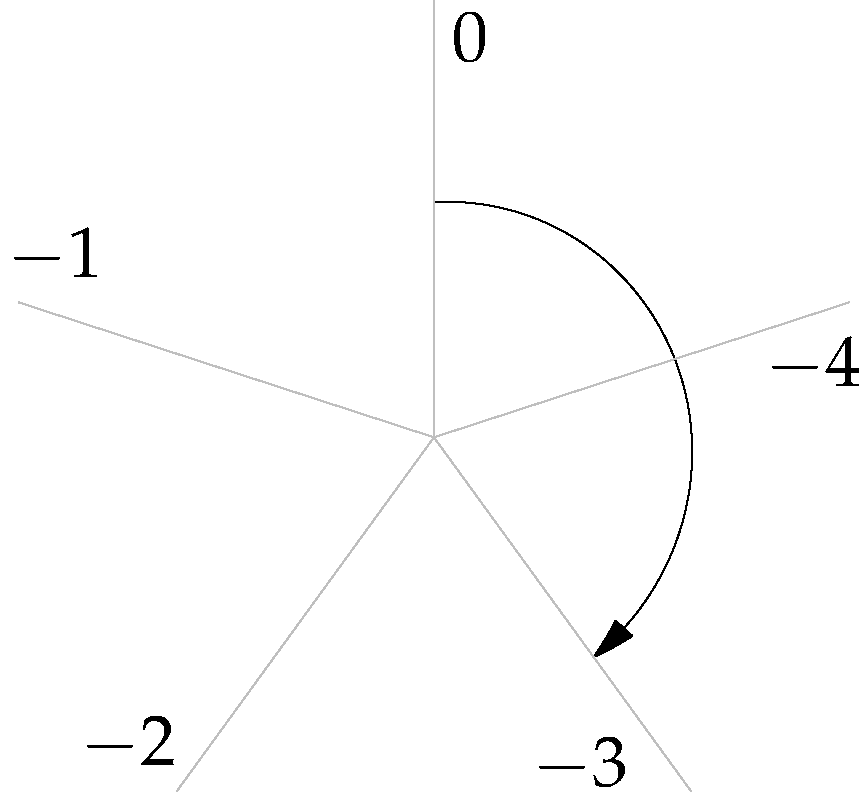
Figure 12: 2 + 4 \equiv -4 \pmod {-5}

We can confirm these agree with Python’s evaluation of these expressions:

>>> 1 % -5
-4
>>> 2 % -5
-3
>>> (4 + 2) % -5
-4

Why did I put (4 + 2) in parentheses? Because % has higher precedence than +. Again, try inputting your own expressions into the Python shell.

Some things to note

  • If the modulus is an integer, n > 0, then the only possible remainders are [0, 1, ..., n - 1].
  • If the modulus is an integer, n < 0, then the only possible remainders are [n + 1, ..., -1, 0].

What now?

This is actually a big topic, involving equivalence classes, remainders (in this context, called “residues”), and others. That’s all outside the scope of this textbook. Practically, however, there are abundant applications for modular arithmetic, and this is something we’ll see again and again in this text.

Some applications for modular arithmetic include:

  • Hashing function
  • Cryptography
  • Primality and divisibility testing
  • Number theory

Here are a couple of simple examples.

Example: eggs and cartons

Jenny has n eggs. If a carton holds 12 eggs, how many complete cartons can she make and how many eggs will be left over?

EGGS_PER_CARTON = 12
cartons = n // EGGS_PER_CARTON
leftover = n % EGGS_PER_CARTON

Example: even or odd

Given some integer n is n even or odd?

if n % 2 == 0:
    print(f'{n} is even')
else:
    print(f'{n} is odd')

(Yes, there’s an even simpler way to write this. We’ll get to that in due course.)

Comprehension check

  1. Given some modulus, n, an integer, and some dividend, d, also an integer, what are the possible values of d % n if

    1. n = 5
    2. n = -4
    3. n = 2
    4. n = 0

  2. Explain why, if the modulus is positive, the remainder can never be greater than the modulus.

  3. The planet Zorlax orbits its sun every 291 1/3 Zorlaxian days. Thus, starting from the year 1, every third year is a leap year on Zorlax. So the year 3 is a leap year. The year 6 is a leap year. The year 273 is a leap year. Write a Python expression which, given some integer y greater than or equal to 1 representing the year, will determine whether y represents a Zorlaxian leap year.

  4. There’s a funny little poem: Solomon Grundy— / Born on a Monday, / Christened on Tuesday, / Married on Wednesday, / Took ill on Thursday, / Grew worse on Friday, / Died on Saturday, / Buried on Sunday. / That was the end / Of Solomon Grundy.4 How could this be? Was Solomon Grundy married as an infant? Did he die before he was a week old? What does this have to do with modular arithmetic? What if I told you that Solomon Grundy was married at age 28, and died at age 81? Explain.

Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >

No generative AI was used in producing this material. This was written the old-fashioned way.

This material is for free use under either the GNU Free Documentation License or the Creative Commons Attribution-ShareAlike 3.0 United States License (take your pick).

Footnotes

  1. Euclid had many things named after him, even if he wasn’t the originator (I guess fame begets fame). Anyhow, Euclid was unaware of the division algorithm you’re taught in primary school. Similar division algorithms depend on the positional system of Hindu-Arabic numerals, and these date from around the 12th Century CE. The algorithm you most likely learned, called “long division”, dates from around 1600 CE.↩︎

  2. https://docs.python.org/3/reference/expressions.html↩︎

  3. OK. Maybe in the military or in Europe you might, but you get the idea. We have a clock with numbers 12–11, and 12 hours brings us back to where we started (at least as far as the clock face is concerned). Notice also that the arithmetic is the same for an analog clock face with hands and a digital clock face. This difference in interface doesn’t change the math at all, it’s just that visually things work out nicely with the analog clock face.↩︎

  4. First recorded by James Orchard Halliwell and published in 1842. Minor changes to punctuation by the author.↩︎