Introduction to binary numbers and binary arithmetic
Introduction to binary numbers
You may know that computers use binary code to represent, well … everything. Everything stored on your computer’s disk or solid-state drive is stored in binary form, a sequence of zeros and ones. All the programs your computer runs are sequences of zeros and ones. All the photos you save, all the music you listen to, even your word processing documents are all zeros and ones. Colors are represented with binary numbers. Audio waveforms are represented with binary numbers. Characters in your word processing document are represented with binary numbers. All the instructions executed and data processed by your computer are represented in binary form.
Accordingly, as computer scientists, we need to understand how we represent numbers in binary form and how we can perform arithmetic operations on such numbers.
However, first, let’s review the familiar decimal system.
The decimal system
We’ve all used the decimal system.
The decimal system is a positional numeral system based on powers of ten.1 What do we mean by that? In the decimal system, we represent numbers as coefficients in a sequence of powers of ten, where each coefficient appears in a position which corresponds to a certain power of ten. (That’s a mouthful, I know.) This is best explained with an example.
Take the (decimal) number 8,675,309. Each digit is a coefficient in the sequence
\begin{equation*} 8 \times 10^6 + 6 \times 10^5 + 7 \times 10^4 + 5 \times 10^3 + 3 \times 10^2 + 0 \times 10^1 + 9 \times 10^0 \end{equation*}
Recall that anything to the zero power is one—so, 10^0 = 1. If we do the arithmetic we get the correct result:
\begin{align*} 8 \times 10^6 = 8{,}000{,}000 \\ 6 \times 10^5 = {\color{white}0{,}}600{,}000 \\ 7 \times 10^4 = {\color{white}0{,}0}70{,}000 \\ 5 \times 10^3 = {\color{white}0{,}00}5{,}000 \\ 3 \times 10^2 = {\color{white}0{,}000{,}}300 \\ 0 \times 10^1 = {\color{white}0{,}000{,}0}00 \\ 9 \times 10^0 = {\color{white}0{,}000{,}00}9 \end{align*}
and all that adds up to 8,675,309.
This demonstrates the power and conciseness of a positional numeral system.
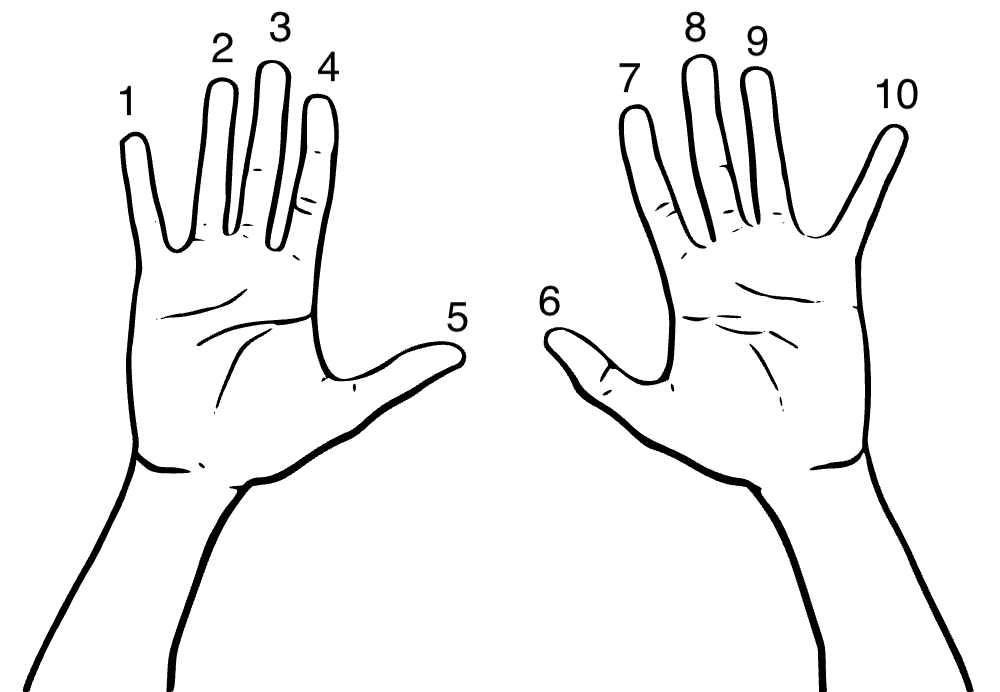
Notice that if we use base 10 for our system we need ten numerals to use as coefficients. For base 10, we use the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
However, apart from the fact that most of us conveniently have ten fingers to count on, the choice of 10 as a base is arbitrary.
Computers and the binary system
As noted, computers use the binary system. This choice was originally motivated by the fact that electronic components which can be in one of two states are generally easier to design and implement than components that can be in one of more than two states.
So how does the binary system work? It, too, is a positional numeral system, but instead of using 10 as a base we use 2.
When using base 2, we need only two numerals: 0 and 1.
In the binary system, we represent numbers as coefficients in a sequence of powers of two. As with the decimal system, this is best explained with an example.
Take the decimal number 975. In binary this is 1111001111. That’s
\begin{align*} 1 \times 2^9 &+ 1 \times 2^8 + 1 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 \\ \hspace{3em} &+\; 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 \end{align*}
Again, doing the arithmetic
\begin{align*} 1 \times 2^9 = 1000000000 \\ 1 \times 2^8 = {\color{white}0}100000000 \\ 1 \times 2^7 = {\color{white}00}10000000 \\ 1 \times 2^6 = {\color{white}000}1000000 \\ 0 \times 2^5 = {\color{white}0000}000000 \\ 0 \times 2^4 = {\color{white}00000}00000 \\ 1 \times 2^3 = {\color{white}000000}1000 \\ 1 \times 2^2 = {\color{white}0000000}100 \\ 1 \times 2^1 = {\color{white}00000000}10 \\ 1 \times 2^0 = {\color{white}000000000}1 \end{align*}
and that all adds up to 1111001111. To verify, let’s represent these values in decimal format and check our arithmetic.
\begin{align*} 1 \times 2^9 = 512 \\ 1 \times 2^8 = 256 \\ 1 \times 2^7 = 128 \\ 1 \times 2^6 = {\color{white}0}64 \\ 0 \times 2^5 = {\color{white}00}0 \\ 0 \times 2^4 = {\color{white}00}0 \\ 1 \times 2^3 = {\color{white}00}8 \\ 1 \times 2^2 = {\color{white}00}4 \\ 1 \times 2^1 = {\color{white}00}2 \\ 1 \times 2^0 = {\color{white}00}1 \end{align*}
Indeed, this adds to 975.
Where in the decimal system we have the ones place, the tens place, the hundreds place, and so on, in the binary system we have the ones place, the twos place, the fours place, and so on.
How would we write, in binary, the decimal number 3? 11. That’s one two, and one one.
How about the decimal number 10? 1010. That’s one eight, zero fours, one two, and zero ones.
How about the decimal number 13? 1101. That’s one eight, one four, zero twos, and one one.
Binary arithmetic
Once you get the hang of it, binary arithmetic is straightforward. Here’s the most basic example: adding 1 and 1.
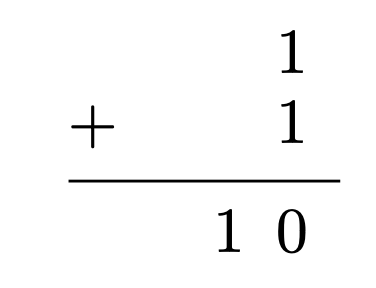
In the ones column we add one plus one, that’s two—binary 10—so we write 0, carry 1 into the twos column, and then write 1 in the twos column, and we’re done.
Now let’s add 1011 (decimal 11) and 11 (decimal 3).
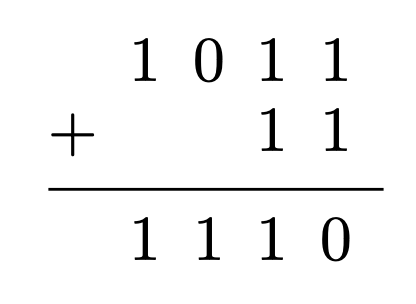
In the ones column we add one plus one, that’s two—binary 10—so we write 0 and carry 1 into the twos column. Then in the twos column we add one (carried) plus one, plus one, that’s three—binary 11—so we write 1 and carry 1 into the fours column. In the fours column we add one (carried) plus zero, so we write 1, and we have nothing to carry. In the eights column we have only the single eight, so we write that, and we’re done. To verify (in decimal):
\begin{align*} 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 &=\; 1 \times 8 + 1 \times 4 + 1 \times 2 + 0 \times 1\\ &=\; 14 \end{align*}
That checks out.
Original author: Clayton Cafiero < [given name] DOT [surname] AT uvm DOT edu >
No generative AI was used in producing this material. This was written the old-fashioned way.
This material is for free use under either the GNU Free Documentation License or the Creative Commons Attribution-ShareAlike 3.0 United States License (take your pick).
Footnotes
In fact, the first positional numeral system, developed in ancient Babylonia around 2000 BCE, used 60 as a base. Our base 10 system is an extension of the Hindu-Arabic numeral system. Other cultures have used other bases. For example, the Kewa counting system in Papua New Guinea is base 37—counting on fingers and other parts of the body: heel of thumb, palm, wrist, forearm, etc, up to the top of the head, and then back down the other side! See: Wolfers, E. P. (1971). “The Original Counting Systems of Papua and New Guinea”, The Arithmetic Teacher, 18(2), 77-83, https://www.jstor.org/stable/41187615.↩︎